题目内容
【题目】在平面直角坐标系![]() 中,抛物线
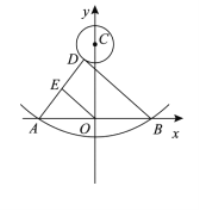
中,抛物线![]() 与x轴的交点为A,B,与y轴交于C.
与x轴的交点为A,B,与y轴交于C.
(1)求抛物线的对称轴和点C坐标;
(2)横、纵坐标都是整数的点叫做整点.拋物线在点A,B之间的部分与线段![]() 所围成的区域为图形W(不含边界).
所围成的区域为图形W(不含边界).
①当![]() 时,求图形W内的整点个数;
时,求图形W内的整点个数;
②若图形W内有2个整数点,求m的取值范围.
【答案】(1)抛物线的对称轴为![]() ,
,![]() ;(2)①1个;②
;(2)①1个;②![]() .
.
【解析】
(1)先根据二次函数的对称轴![]() 可得其对称轴,再令
可得其对称轴,再令![]() ,求出y的值,从而可得出点C坐标;
,求出y的值,从而可得出点C坐标;
(2)①先得出抛物线的解析式,再画出图象,结合图象和整点的定义即可得;
②先将二次函数的解析式化为顶点式,求出其顶点坐标,再结合图象,找出两个临界位置,分别求出m的值,由此即可得出答案.
(1)抛物线![]() 的对称轴为
的对称轴为![]()
令![]() 得:
得:![]()
则点C坐标为![]() ;
;
(2)①当![]() 时
时
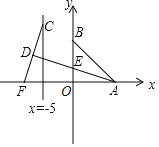
![]() ,画出其图象如下所示:
,画出其图象如下所示:
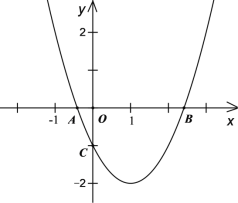
结合图象和整点的定义可得:图形W内的整点只有1个,即点![]() ;
;
②将抛物线![]() 化为顶点式
化为顶点式![]()
则抛物线的顶点坐标为![]() ,且图象经过定点
,且图象经过定点![]()
结合图象可知,若图形W内的整点有2个,则这两个整点只能是![]()
因此有两个临界点:抛物线顶点为![]() 和抛物线顶点为
和抛物线顶点为![]()
当抛物线顶点为![]() 时,
时,![]() ,解得
,解得![]()
当抛物线顶点为![]() 时,
时,![]() ,解得
,解得![]()
则m的取值范围为![]() .
.


【题目】某商场在端午节前以1元/个的价格购进1000个粽子,现有以下三种销售方式:不加工直接卖,对产品进行粗加工后再卖,对产品进行精加工后再卖.受加工能力和气温影响,粗加工一天只能加工200个,细加工一天只能加工100个,两种加工不能同时进行,且最多加工三天.
加工方式 | 加工成本 | 销售单位 | 售价 |
直接卖 | 0 | 个 | 2元/个 |
粗加工 | 1元/个 | 包装袋(一袋5个) | 30元/袋 |
精加工 | 2.5元/个 | 礼盒(一盒10个) | 85元/盒 |
假设所有粽子均能全部售出,则以下销售方式中利润最大的是____________.
方案一:不加工直接销售;
方案二:三天全部进行精加工,剩下的直接卖;
方案三:两天精加工,一天粗加工,剩下的直接卖;
方案四:两天粗加工,一天精加工,剩下的直接卖.