��Ŀ����
����Ŀ���Ķ������ں���y=ax2+bx+c��a��0������t1��x��t2ʱ����y����ֵʱ����Ҫȡ���ڶԳ���x=�� ![]() �Ƿ���t1��x��t2�ķ�Χ��a���������ٵ��Գ���x=��
�Ƿ���t1��x��t2�ķ�Χ��a���������ٵ��Գ���x=�� ![]() ��t1��x��t2֮����a��0ʱ����x=��
��t1��x��t2֮����a��0ʱ����x=�� ![]() ʱy����Сֵ��x=t1��x=t2ʱy�����ֵ���ڵ��Գ���x=��
ʱy����Сֵ��x=t1��x=t2ʱy�����ֵ���ڵ��Գ���x=�� ![]() ��t1��x��t2֮����a��0ʱ����x=��
��t1��x��t2֮����a��0ʱ����x=�� ![]() ʱy�����ֵ��x=t1��x=t2ʱy����Сֵ���۵��Գ���x=��
ʱy�����ֵ��x=t1��x=t2ʱy����Сֵ���۵��Գ���x=�� ![]() ����t1��x��t2֮�ڣ�������x=t1��x=t2ʱy����ֵ��
����t1��x��t2֮�ڣ�������x=t1��x=t2ʱy����ֵ��
������⣺
����κ���y1=a��x��2��2+c��a��0����ͼ����y��Ľ���Ϊ��0��1������2a+c=0��
��1����a��c��ֵ��
��2������2��x��1ʱ��ֱ��д�����������ֵ����Сֵ��
��3����������ʵ��k���涨������2��x��1ʱ������x�ĺ���y2=y1��kx����Сֵ��Ϊk�ġ��ر�ֵ��������g��k������g��k���Ľ���ʽ��
��4���ڣ�3���������£������ر�ֵ��g��k��=1ʱ����k��ֵ��
���𰸡�
��1���⣺����0��1������ã�4a+c=1��
�֡�2a+c=0��
��2a=1����ã�a= ![]() ��
��
��c=��2a=��2�� ![]() =��1��
=��1��
��2���⣺��a= ![]() ��c=��1��
��c=��1��
��y1= ![]() ��x��2��2��1��
��x��2��2��1��
��x=�� ![]() =2��
=2��
��x=2���ک�2��x��1֮�ڣ�
�൱x=��2ʱ��y1�����ֵ�����ֵΪ= ![]() ��16��1=7����x=1ʱ��y1����Сֵ����СֵΪ=
��16��1=7����x=1ʱ��y1����Сֵ����СֵΪ= ![]() ��1��1=��
��1��1=�� ![]()
��3���⣺��y2=y1��kx��
��y2= ![]() ��x��2��2��1=��kx=
��x��2��2��1=��kx= ![]() x2����k+2��x+1��
x2����k+2��x+1��
�������ߵĶԳ���Ϊx=k+2��
��k+2����2ʱ����k����4ʱ����x=��2ʱ��y2����Сֵ��y2����Сֵ= ![]() ��4+2��k+2��+1=2k+7��
��4+2��k+2��+1=2k+7��
����2��k+2��1ʱ������4��k�ܩ�1ʱ����x=k+2ʱ��y2����Сֵ��y2����Сֵ= ![]() ��k+2��2����k+2��2+1=��
��k+2��2����k+2��2+1=�� ![]() ��k+2��2+1��
��k+2��2+1��
��k+2��1ʱ����k����1ʱ����x=1ʱ��y2����Сֵ��y2����Сֵ= ![]() ��1����k+2��+1=��k��
��1����k+2��+1=��k�� ![]() ��
��
����������g��k���Ľ���ʽΪg��k��= 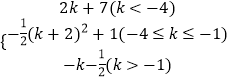
��4���⣺��k����4ʱ����y=2k+7=1����k=��3������������ȥ��
����4��k�ܩ�1ʱ����y=�� ![]() ��k+2��2+1=1����k=��2��
��k+2��2+1=1����k=��2��
��k����1ʱ����y=��k�� ![]() =1����k=��
=1����k=�� ![]() ����ȥ��
����ȥ��
����������k=��2��
����������1������0��1������ã�4a+c=1��Ȼ��4a+c=1��2a+c=0���������a��c��ֵ����2����a= ![]() ��c=��1�����y1=
��c=��1�����y1= ![]() ��x��2��2��1�������ߵĶԳ���Ϊx=2��Ȼ���ک�2��x��1��Χ�ڣ���x=��2ʱ��y1�д�ֵ����x=1ʱ��y1����Сֵ����3���������֪y2=
��x��2��2��1�������ߵĶԳ���Ϊx=2��Ȼ���ک�2��x��1��Χ�ڣ���x=��2ʱ��y1�д�ֵ����x=1ʱ��y1����Сֵ����3���������֪y2= ![]() x2����k+2��x+1�������ߵĶԳ���Ϊx=k+2��Ȼ���Ϊk+2����2����2��k+2��1��k+2��1��������ֱ����y2����Сֵ���ɣ���4����g��k��=1�г�����k�ķ��̣��Ӷ������k��ֵ��
x2����k+2��x+1�������ߵĶԳ���Ϊx=k+2��Ȼ���Ϊk+2����2����2��k+2��1��k+2��1��������ֱ����y2����Сֵ���ɣ���4����g��k��=1�г�����k�ķ��̣��Ӷ������k��ֵ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�