题目内容
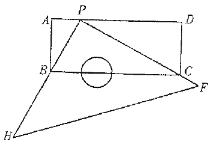
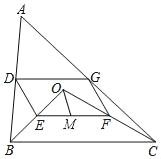
【题目】如图,点O是△ABC内一点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=3,求DG的长度.
【答案】(1)证明见解析;(2)6
【解析】
(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=![]() BC,DG∥BC且DG=
BC,DG∥BC且DG=![]() BC,从而得到DG=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可.
BC,从而得到DG=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可.
(2)想办法证明OM=MF=ME即可解决问题.
(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=![]() BC,
BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=![]() BC,
BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)∵OB⊥OC,
∴∠BOC=90°,
∵∠EOM+∠COM=90°,∠EOM+∠OCB=90°,
∴∠COM=∠OCB,
∵EF∥BC,
∴∠OFE=∠OCB,
∴∠MOF=∠MFO,
∴OM=MF,
∵∠OEM+∠OFM=90°,∠EOM+∠MOF=90°,
∴∠EOM=∠MEO,
∴OM=EM,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目