题目内容
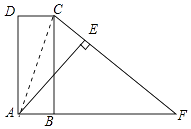
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E. 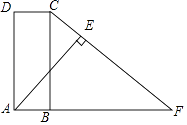
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.
【答案】
(1)证明:连接AC,如图所示:
∵CF=AF,∴∠FCA=∠CAF,
∵四边形ABCD是矩形,∴DC∥AB∴,∠DCA=∠CAF,
∴∠FCA=∠DCA,
∵AE⊥FC,
∴∠CEA=90°,
∴∠CDA=∠CEA=90°,
在△ADC和△CAE 中, 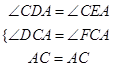 ,
,
∴△ADC≌△CAE (AAS),
∴AD=AE;
(2)解:∵△ADC≌△CAE,
∴∠CAE=∠CAD,
∵四边形ABCD是矩形,
∴∠D=90°,
∴∠CAD=90°﹣∠DCA=90°﹣70°=20°,
∴∠CAE=20°.
【解析】(1)由等腰三角形的性质和矩形的性质证出∠FCA=∠DCA,由AAS证明△ADC≌△CAE,即可得出结论;(2)由全等三角形的性质得出∠CAE=∠CAD,求出∠CAD=90°﹣∠DCA=20°,即可得出答案.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).

练习册系列答案
相关题目