��Ŀ����
����Ŀ���Ķ���������:
����֪��������һ��ͼ�Σ�ͨ�����ֲ�ͬ�ķ�������������������Եõ�һ����ѧ��ʽ����������ͼ���������ɸ��߳�Ϊ![]() �ͱ߳�Ϊ
�ͱ߳�Ϊ![]() ��С������ֽƬ�����ɸ��߳�Ϊ
��С������ֽƬ�����ɸ��߳�Ϊ![]() �ij�����ֽƬ����ͼ������ͼ�ṩ�ļ���ͼ��ƴ�Ӷ��ã����Եõ�
�ij�����ֽƬ����ͼ������ͼ�ṩ�ļ���ͼ��ƴ�Ӷ��ã����Եõ�![]()
![]()
�����������⣺
(1)��д����ͼ������ʾ����ѧ��ʽ��______________________________��
(2)��(1)�����õ��Ľ���,������������:��֪![]() ��
��![]() ��ֵΪ_________.
��ֵΪ_________.
(3)���밴Ҫ������������ֽƬƴ��һ�������Σ�Ҫ����ƴ��ͼ�ε����Ϊ![]() ������ƴ����ͼ���ڵķ����У�
������ƴ����ͼ���ڵķ����У�
����������һ�ּ�������ķ���,�ɽ�����ʽ![]() �ֽ���ʽ����
�ֽ���ʽ����![]() _________.
_________.

���𰸡���1����a+b+c��2=a2+b2+c2+2ab+2bc+2ac;��2��45��3���ټ������� (2a+b)(a+b)
��������
��1�����ݷָ�������ķ�������д����ʽ����a+b+c��2=a2+b2+c2+2ab+2bc+2ac;
��2�����ݣ�1���еĵ�ʽֱ�Ӵ��뼴���������3���ٸ������⻭��ƴ����ͼ�Σ�ʹ�����Ϊ![]() ���ڸ�����ƴ��ͼ�����þ��ε�������ɰ�
���ڸ�����ƴ��ͼ�����þ��ε�������ɰ�![]() �ֽ���ʽ.
�ֽ���ʽ.
��1����a+b+c��2=a2+b2+c2+2ab+2bc+2ac;
��2����![]()
��![]() =��a+b+c��2-2(ab+bc+ac)=112-2��38=45
=��a+b+c��2-2(ab+bc+ac)=112-2��38=45
��3������ͼ��
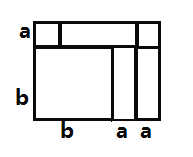
��![]() =(2a+b)(a+b)
=(2a+b)(a+b)

 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�