题目内容
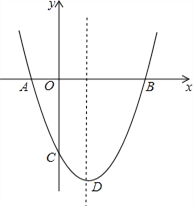
【题目】已知抛物线![]() 与x轴交于两点A、
与x轴交于两点A、![]() 点A在x轴的正半轴上,点B在x轴的负半轴上
点A在x轴的正半轴上,点B在x轴的负半轴上![]() 与y轴交于点C.
与y轴交于点C.
![]() 求m的取值范围;
求m的取值范围;
![]() 如果
如果![]() :
:![]() :1,在该抛物线对称轴右边图象上求一点P的坐标,使得
:1,在该抛物线对称轴右边图象上求一点P的坐标,使得![]() .
.
【答案】(1)m>-3;(2)![]() 点坐标为
点坐标为![]() .
.
【解析】试题分析:
(1)由题意可得△=![]() ,说明抛物线与x轴总有两个不同的交点,由此根据抛物线与x轴的两个交点位于原点左、右两侧可得:-(m+3)<0,由此即可解得m的取值范围;
,说明抛物线与x轴总有两个不同的交点,由此根据抛物线与x轴的两个交点位于原点左、右两侧可得:-(m+3)<0,由此即可解得m的取值范围;
(2)设线段OB=k,则线段OA=3k,由题意可得点A的坐标为(3k,0),点B的坐标为(-k,0),则3k和-k是一元二次方程![]() 的两根,由一元二次方程根与系数的关系列出方程组,解方程组即可求得k和m的值,从而可得点B的坐标和抛物线的解析式,设PC和x轴的交点为D,由∠PCO=∠BCO,可得点D和点B关于原点对称,由此可得点D的坐标,从而可的直线PC的解析式,由PC的解析式和抛物线的解析式组成方程组,解方程组即可求得点P的坐标.
的两根,由一元二次方程根与系数的关系列出方程组,解方程组即可求得k和m的值,从而可得点B的坐标和抛物线的解析式,设PC和x轴的交点为D,由∠PCO=∠BCO,可得点D和点B关于原点对称,由此可得点D的坐标,从而可的直线PC的解析式,由PC的解析式和抛物线的解析式组成方程组,解方程组即可求得点P的坐标.
试题解析:
(1)∵抛物线![]() 中,
中,
△=![]() ,
,
∴该抛物线与x轴总有两个不同的交点,
又∵该抛物线与x轴的两个交点一个在原点左边,一个在原点右边,
∴-(m+3)<0,解得:m>-3;
(2)设![]() ,则由题意可得
,则由题意可得![]() ,点A、B的坐标分别为:(3k,0)、(-k,0),
,点A、B的坐标分别为:(3k,0)、(-k,0),
∴-k和3k是一元二次方程![]() 的两根,
的两根,
∴![]() ,解得:
,解得: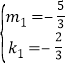 (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴抛物线的解析式为:![]() ,点B的坐标为(-1,0),点C的坐标为(0,3),
,点B的坐标为(-1,0),点C的坐标为(0,3),
如图,设点B关于原点的对称点是点D,则点D的坐标为(1,0),连接CD并延长交抛物线于点P,则此时∠PCO=∠BCO,
由点C的坐标为(0,3)、点D的坐标为(1,0)可得直线CD的解析式为:![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() ,
,
∵点P不能与点C重合,
∴点P的坐标为(5,-12).

练习册系列答案
相关题目