题目内容
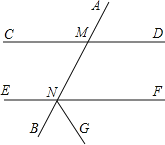
【题目】已知图,正方形ABCD,M是BC延长线上一点,过B作BE⊥DM于点E,交DC于点F,过F作FG∥BC交BD于点G,连接GM,若S△EFD= ![]() DF2 , AB=4
DF2 , AB=4 ![]() ,则GM= .
,则GM= . 
【答案】8( ![]() ﹣1)
﹣1)
【解析】解:如图,作EH⊥CD于H,CN⊥DM于N,NK⊥CD于K.
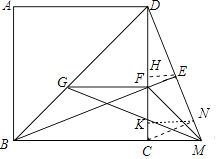
∵四边形ABCD是正方形,
∴∠BCF=∠DCM=90°,BC=DC,
∵BE⊥DM,
∴∠BEM=90°,
∴∠CBF+∠BME=90°,∠BME+∠CDM=90°,
∴∠CBF=∠CDM,
∴△BCF≌△DCM,
∴BF=DM,CF=CM,
∴∠FMB=∠GBM=45°,
∵FG∥BM,
∴四边形BMFG是等腰梯形,
∴GM=BF=DM,
∵S△DEF= ![]() DFEH=
DFEH= ![]() DF2,
DF2,
∴EH= ![]() DF,即DF=4EH,
DF,即DF=4EH,
∵△DEF∽△DNC∽△DCM,
∴CD=4NK,DM=4CN,
∵AB=CD=4 ![]() ,
,
∴NK= ![]() ,设CK=x,则DK=4
,设CK=x,则DK=4 ![]() ﹣x,
﹣x,
∵△DKN∽△NKC,
∴NK2=DKKC,
∴2=x(4 ![]() ﹣x),
﹣x),
∴x=2 ![]() ﹣
﹣ ![]() 或2
或2 ![]() +
+ ![]() (舍弃),
(舍弃),
在Rt△CKN中,CN= ![]() =
= ![]() =2(
=2( ![]() ﹣1),
﹣1),
∴GM=DM=4CN=8( ![]() ﹣1).
﹣1).
所以答案是8( ![]() ﹣1).
﹣1).
【考点精析】掌握三角形的面积和勾股定理的概念是解答本题的根本,需要知道三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目