题目内容
【题目】在△ABC中,点E、F在边BC上,点D在边AC上,连接ED、DF,![]() =m,∠A=∠EDF=120°
=m,∠A=∠EDF=120°
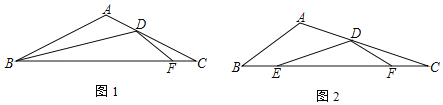
(1)如图1,点E、B重合,m=1时
①若BD平分∠ABC,求证:CD2=CFCB;
②若![]() ,则
,则![]() = ;
= ;
(2)如图2,点E、B不重合.若BE=CF,![]() =m,
=m,![]() ,求m的值.
,求m的值.
【答案】(1)①见解析;②![]() 或
或![]() ;(2)m=
;(2)m=![]() .
.
【解析】
(1)①由三角形的外角性质和角平分线性质可得∠ABD=∠CDF=∠DBF,可证△CDF∽△CBD,可得![]() ,即可得结论;
,即可得结论;
②如图1,作辅助线,构建一线三等角,证明△ABD∽△HDF,得![]() ,即
,即![]() ,设AD=x,则DH=11a﹣x,列方程解出可得x=5a或6a,代入可得结论;
,设AD=x,则DH=11a﹣x,列方程解出可得x=5a或6a,代入可得结论;
(2)如图2,作辅助线,构建平行线和相似三角形,先证明△ABC∽△DFE,得∠DEC=∠C,所以DE=DC,设未知数,表示EH和CH的长,根据平行线分线段成比例定理由:m=![]() 代入可得结论.
代入可得结论.
(1)①∵![]() ,
,
∴AB=AC,
∵BD平分∠ABC,
∴∠ABD=∠DBF,
∵∠BDC=∠A+∠ABD=∠BDF+∠CDF,且∠A=∠BDF=120°,
∴∠ABD=∠CDF=∠DBF,且∠C=∠C,
∴△CDF∽△CBD,
∴![]() ,
,
∴CD2=BCCF;
②如图1,过A作AG⊥BC于G,过F作FH⊥BC,交AC于H,
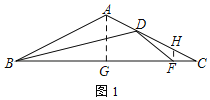
∵∠C=30°,
∴CH=2FH,
设FH=2a,CH=4a,则CF=2![]() a,
a,
∵![]() ,
,
∴BC=15![]() a,
a,
∵CG=![]() a,
a,
∴AG=![]() a,AC=15a,
a,AC=15a,
∴AH=11a,
∵∠BAD=∠BDF=∠DHF=120°,
∴∠ADB+∠FDH=∠ADB+∠ABD=180°﹣120°=60°,
∴∠ABD=∠FDH,
∴△BD∽△HDF,
∴![]() ,即
,即![]() ,
,
设AD=x,则DH=11a﹣x,
∴30a2=x(11a﹣x),
x2﹣11ax+30a2=0,
(x﹣5a)(x﹣6a)=0,
x=5a或6a,
∴![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() ;
;
(2)如图2,过E作EH∥AB,交AC于H,过D作DM⊥EH于M,过F作FG∥ED,交AC于G,
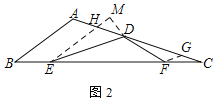
∵BE=CF,![]() ,
,
∴![]() ,
,
∵FG∥ED,
∴![]() ,
,
∴设CG=3a,DG=7a,
∵![]() m,∠A=∠EDF=120°,
m,∠A=∠EDF=120°,
∴△ABC∽△DFE,
∴∠DEC=∠C,
∴DE=DC=10a,
∵FG∥DE,
∴∠GFC=∠DEF=∠C,
∴FG=CG=3a,
同理由(1)得:△EHD∽△DFG,
∴![]() ,即
,即![]() ,
,
DH=![]() ,
,
Rt△DHM中,∠DHM=60°,
∴∠HDM=30°,
∴HM=![]() DH=
DH=![]() ,DM=
,DM=![]() a,
a,
∴EM=![]() ,
,
∴EH=![]() ﹣
﹣![]() =
=![]() ,
,
∴m=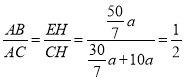 .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
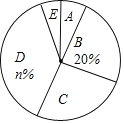
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上的信息,回答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %.
(2)被调查学生的总数为 人,统计表中m的值为 ,统计图中n的值为 .
(3)在统计图中,E类所对应扇形圆心角的度数为 .
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.