题目内容
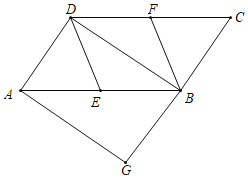
【题目】如图,正方形ABCD中,点E、F分别在AB、CD上,DG⊥EF于点H,交BC于点G,点P在线段BG上.若∠PEF=45°,AE=CG=5,PG=5,则EP=____.

【答案】5![]() .
.
【解析】
过点F作FM⊥AB于点M,连接PF、PM,则FM=AD,AM=DF,由ASA证明△MCE≌△CDG,得出ME=CG=5,得出AM=DF=10,证明E、M、P、F四点共圆,得出∠EPF=∠FME=90°,证出△PEF是等腰直角三角形,得出EP=FP,证明△BPE≌△CFP,得出BE=CP=10,求出AB=AE+BE=15,BP=5,在Rt△BPE中,由勾股定理即可得出结果.
过点F作FM⊥AB于点M,连接PF、PM,如图所示:
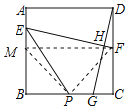
则FM=AD,AM=DF,∠FME=∠MFD=90°,
∵DG⊥EF,
∴∠MFE=∠CDG,
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=DC=AD,
∴FM=DC,
在△MCE和△CDG中, ,
,
∴△MCE≌△CDG(ASA),
∴ME=CG=5,
∴AM=DF=10,
∵CG=PG=5,
∴CP=10,
∴AM=CP,
∴BM=BP,
∴△BPM是等腰直角三角形,
∴∠BMP=45°,
∴∠PMF=45°,
∵∠PEF=45°=∠PMF,
∴E、M、P、F四点共圆,
∴∠EPF=∠FME=90°,
∴△PEF是等腰直角三角形,
∴EP=FP,
∵∠BEP+∠BPE=90°,∠BPE+∠CPF=90°,
∴∠BEP=∠CPF,
在△BPE和△CFP中,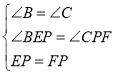 ,
,
∴△BPE≌△CFP(AAS),
∴BE=CP=10,
∴AB=AE+BE=15,
∴BP=5,
在Rt△BPE中,由勾股定理得:EP=![]() =5
=5![]() ;
;
故答案为:5![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目