题目内容
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴相交于点C.连接AC、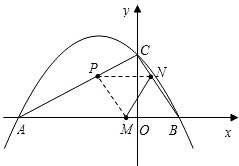 BC,B、C两点的坐标分别为B(1,0)、C(0,
BC,B、C两点的坐标分别为B(1,0)、C(0,
),且当x=-10和x=8时函数的值y相等.
(1)求a、b、c的值;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.连接MN,将△BMN沿MN翻折,当运动时间为几秒时,B点恰好落在AC边上的P处?并求点P的坐标;
(3)上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式.
 BC,B、C两点的坐标分别为B(1,0)、C(0,
BC,B、C两点的坐标分别为B(1,0)、C(0,| 3 |
(1)求a、b、c的值;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.连接MN,将△BMN沿MN翻折,当运动时间为几秒时,B点恰好落在AC边上的P处?并求点P的坐标;
(3)上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式.
(1)∵当x=-10和x=8时函数的值y相等,
∴抛物线的对称轴为直线x=-1.
由题意得:a+b+c=0,c=
,-
=-1,
∴a=-
,b=-
,c=
;(3分)
(2)令y=0,则x=-3或1,∴A(-3,0),
易得AC=2
,BC=2,AB=4.
∴△ABC为直角三角形,∠ACB=90°,∠A=30°,∠B=60°,(1分)
∴BM=BN=PN=PM,
∴四边形BNPM为菱形,
∴PM=BN.
设运动t秒后点B在AC上,
∵PN∥AB,
∴
=
,即
=
,∴t=
.(1分)
∴PM=BN=
,
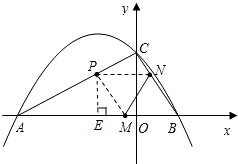
过P作PE⊥AB于E,
在Rt△PEM中,PE=
sin60°=
,
∴OM=BM-OB=
-1=
,OE=1.
∴P(-1,
);
(3)设所求抛物线的解析式为y=-
(x+1)2+k.
Rt△OBC中,∠OBC=60°,
若△ODE与△OBC相似,则:
①∠DOE=60°,
Rt△ODE中,OE=1,则DE=
故D(-1,
)或(-1,-
)
∴平移后的抛物线解析式为:y=-
(x+1)2+
或y=-
(x+1)2-
②∠DOE=30°
Rt△ODE中,OE=1,则DE=
故D(-1,
)或(-1,-
)
∴平移后的抛物线解析式为:y=-
(x+1)2+
或y=-
(x+1)2-
综上所述,存在符合条件的抛物线,且解析式为:
y=-
(x+1)2+
或y=-
(x+1)2-
或y=-
(x+1)2+
或y=-
(x+1)2-
.
∴抛物线的对称轴为直线x=-1.
由题意得:a+b+c=0,c=
| 3 |
| b |
| 2a |
∴a=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)令y=0,则x=-3或1,∴A(-3,0),
易得AC=2
| 3 |
∴△ABC为直角三角形,∠ACB=90°,∠A=30°,∠B=60°,(1分)
∴BM=BN=PN=PM,
∴四边形BNPM为菱形,
∴PM=BN.
设运动t秒后点B在AC上,
∵PN∥AB,
∴
| PN |
| AB |
| CN |
| CB |
| t |
| 4 |
| 2-t |
| 2 |
| 4 |
| 3 |
∴PM=BN=
| 4 |
| 3 |
过P作PE⊥AB于E,
在Rt△PEM中,PE=
| 4 |
| 3 |
2
| ||
| 3 |
∴OM=BM-OB=
| 4 |
| 3 |
| 1 |
| 3 |
∴P(-1,
2
| ||
| 3 |
(3)设所求抛物线的解析式为y=-
| ||
| 3 |
Rt△OBC中,∠OBC=60°,
若△ODE与△OBC相似,则:
①∠DOE=60°,
Rt△ODE中,OE=1,则DE=
| 3 |
故D(-1,
| 3 |
| 3 |
∴平移后的抛物线解析式为:y=-
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
②∠DOE=30°
Rt△ODE中,OE=1,则DE=
| ||
| 3 |
故D(-1,
| ||
| 3 |
| ||
| 3 |
∴平移后的抛物线解析式为:y=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
综上所述,存在符合条件的抛物线,且解析式为:
y=-
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |


练习册系列答案
相关题目
 (1)求m的值;
(1)求m的值;



 标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.
标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.