Question

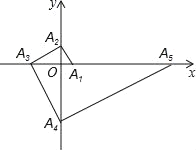
【题目】如图，点A1的坐标为（1，0），A2在y轴的正半轴上，且∠A1A2O＝30°，过点A2作A2A3⊥A1A2垂足为A2，交x轴于点A3过点A3作A3A4⊥A2A3，垂足为A3，交y轴于点A4，过点A4作A4A5⊥A3A4，垂足为A4…交x轴于点A5：过点A5作A5A6⊥A4A5，A5A6⊥A4A5垂足为A5，交y轴于点A6…按此规律进行下去，则点A2019的横坐标为_____．

Answer 1

【答案】﹣31009

【解析】

通过解直角三角形可得出点A2的坐标，同理可得出点A2，A3，A4，A5，A6，A7，…的坐标，根据坐标的变化可得出变化规律“点A4n+3的坐标为（﹣32n+1，0）（n为正整数）”，再结合2019＝504×4+3即可得出点A2019的坐标，此题得解．

∵∠A1A2O＝30°，OA1＝1，

∴OA2＝，

∴点A2的坐标为（0，），

同理，A3（﹣3，0），A4（0，﹣3），A5（9，0），A6（0，9），A7（﹣27，0），…，

∴点A4n+3的坐标为（﹣32n+1，0）（n为正整数）．

∵2019＝504×4+3，

∴点A2019的坐标为（﹣31009，0）．

故答案为：﹣31009．