题目内容
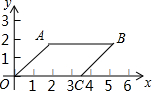
在平行四边形OABC中，已知A，C两点的坐标分别为A（
，
），C（2
，0）．
（1）求B点的坐标．
（2）将平行四边形OABC向左平移
个单位长度，求所得四边形的四个顶点的坐标．
（3）求平行四边形OABC的面积．
| 3 |
| 3 |
| 3 |
（1）求B点的坐标．
（2）将平行四边形OABC向左平移
| 3 |
（3）求平行四边形OABC的面积．
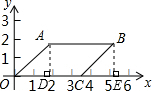
（1）如图，作AD⊥OC于点D，BE⊥OC于E，
∵A（
，
），C（2
，0），
∴BE=AD=
，CE=OD=
，
∴OE=OC+CE=2
+
=3
，
∴B点的坐标是（3
，
）；
（2）将平行四边形ABCO向左平移
个单位长度
四个顶点的坐标分别变为：A′（0，
），B′（2
，
），C′（
，0），O′（-
，0）；
（3）∵OC=2
，AD=
，
∴平行四边形ABCO的面积=OC•AD=2
×
=6．
∵A（
| 3 |
| 3 |
| 3 |
∴BE=AD=
| 3 |
| 3 |
∴OE=OC+CE=2
| 3 |
| 3 |
| 3 |
∴B点的坐标是（3
| 3 |
| 3 |
（2）将平行四边形ABCO向左平移
| 3 |
四个顶点的坐标分别变为：A′（0，
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
（3）∵OC=2
| 3 |
| 3 |
∴平行四边形ABCO的面积=OC•AD=2
| 3 |
| 3 |
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
