题目内容
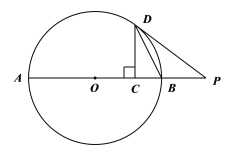
【题目】如图,点D在⊙O上,过点D的切线交直径AB的延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)如果DC = 6,![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结OD,如图,利用切线性质得∠ODB+∠PDB=90°,由CD⊥OB得∠CDB+∠DBC=90°,加上∠ODB=∠OBD,于是得到∠CDB=∠PDB,即DB平分∠PDC;
(2)作BE⊥PD,如图,根据角平分线的性质定理得到BC=BE,在Rt△PDC中,利用三角函数的定义计算PC=8,则利用勾股定理可计算出PD=10,设BC=x,则BE=x,PB=8-x,通过证明Rt△PBE∽Rt△PDC,利用相似比得到x:6=(8-x):10,然后根据比例性质求出x即可.
(1)证明:如图,连接OD.
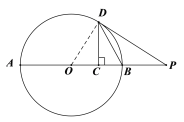
∵ DP是⊙O的切线,
∴ OD⊥DP,
∴ ![]() ,
,
∴ ![]() ,
,
又 ∵DC⊥OB,
∴ ![]() ,
,
∴![]() ,
,
∵OD=OB,
∴![]() ,
,
∴![]() ,
,
∴DB平分∠PDC;
(2)如图,过点B作BE⊥DP于点E.
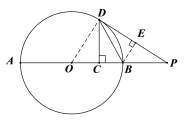
∵![]() ,BC⊥DC,
,BC⊥DC,
∴BC=BE,
∵DC=6,![]() ,
,
∴DP=10,PC=8,
设CB = x,则BE = x,BP = 8 – x,
∵ △PEB∽△PCD,
∴ ![]() ,
,
∴x=3,
∴ ![]() 的长为3.
的长为3.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目