Question

【题目】如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC与点E，将△BCE绕点C顺时针旋转90°得到△DCF，若CE＝1 cm，则BF＝cm.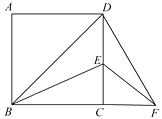

Answer 1

【答案】
【解析】过点E作EM⊥BD于点M,如图所示：

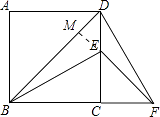
∵四边形ABCD为正方形，

∴∠BAC=45°，∠BCD=90°，

∴△DEM为等腰直角三角形。

∵BE平分∠DBC，EM⊥BD，

∴EM=EC=1cm，

∴DE= EM= cm.

由旋转的性质可知：CF=CE=1cm，

∴BF=BC+CF=CE+DE+CF=1+ +1=2+ cm.

故答案为：2+ .

过点E作EM⊥BD于点M,根据已知条件证明△DEM为等腰直角三角形，再根据角平分线的性质得出EM=EC，根据勾股定理求出DE的长，根据旋转的性质，即可得出结果。