Question

【题目】已知：在矩形ABCD中，AB=4，AD=10，点P是BC上的一点，若∠APD=90°，则AP=_____．

Answer 1

【答案】2或4

【解析】

设BP的长为x，则CP的长为(10-x)，分别在Rt△ABP和Rt△DCP中利用勾股定理用x表示出AP2和DP2，然后在Rt△ADP中利用勾股定理得出关于x的一元二次方程，解出x的值，即可得出AP的长．

解：如图所示：

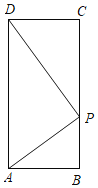
∵四边形ABCD是矩形，

∴∠B=∠C=90°，BC=AD=10，DC=AB=4，

设BP的长为x，则CP的长为(10-x)，

在Rt△ABP中，由勾股定理得：

AP2=AB2+BP2=42+x2，

在Rt△DCP中，由勾股定理得：

DP2=DC2+CP2=42+(10-x)2，

又∵∠APD=90°，

在Rt△APD中，AD2=AP2+DP2，

∴42+x2+42+(10-x)2=102，

整理得：x2-10x+16=0，

解得：x1=2，x2=8，

当BP=2时，AP==；

当BP=8时，AP==．

故答案为：或．