题目内容
如图,直角梯形ABCD置于平面直角坐标系中,BC与x轴重合,点A在y轴上,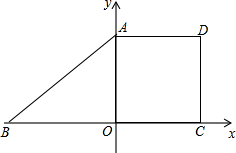 且AD∥BC,AD=CD,若sin∠ABO=
且AD∥BC,AD=CD,若sin∠ABO= ,梯形ABCD的面积为60.
,梯形ABCD的面积为60.
(1)求直线AB的解析式;
(2)若点P从点A出发,沿AB向终点B运动,运动速度为每秒3个单位长度,过点P作AB的垂线交x轴于点E交y轴于点F,设点P的运动时间为t秒,线段EF长为y,求y与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,连接DE、DF,当cos∠EDF= 时,求t的值.
时,求t的值.
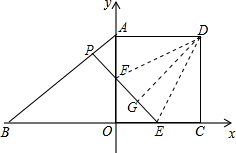 解:(1)∵梯形ABCD是直角梯形,且AD∥BC,∠D=90°,AD=CD,
解:(1)∵梯形ABCD是直角梯形,且AD∥BC,∠D=90°,AD=CD,∴四边形ADCO为正方形,
∴AD=OA=OC.
又∵sin∠ABO=
 ,
,∴
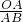 =
= ,
,∴
 =
= ,
,∴OA=
 OB,
OB,∴S梯形ABCD=
 (AD+OB+OC)•OA=
(AD+OB+OC)•OA= ×
× OB×
OB× OB=60,
OB=60,∴OB=8,
∴OA=6,
∴A(0,6),B(-8,0).
设直线AB的解析式为:y=kx+b(k≠0),则
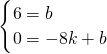 ,
,解得
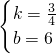 ,
,故直线AB的解析式为:y=
 x+6;
x+6;(2)∵OA=6,OB=8,
∴AB=
 =10.
=10.∵PE⊥AB,
∴cos∠PAF=
 =
=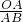 ,即
,即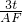 =
=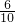 ,
,解得,AF=5t.
∴根据勾股定理求得PF=4t.
∴cos∠OFE=cos∠PFA,即
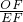 =
=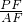 ,
,∴
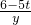 =
=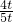 ,
,∴y=-
 t+
t+ (0≤t<
(0≤t< );
);(3)∵
 =
=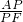 ,
,∴
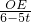 =
=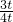 ,即OE=
,即OE= (6-5t),
(6-5t),∴CE=OC-OE=6-
 (6-5t)=
(6-5t)= +
+ t.
t.∵cos∠EDF=
 ,cos∠EDF是锐角,
,cos∠EDF是锐角,∴cos∠EDF=45°.
∵∠ADF+∠CDE=45°,
∴点A关于直线DE的对称点与点C关于直线DE的对称点重合,即图中的点G,
∴AF+CE=FG+CG=EF,即AF+CE=EF.
∴5t+
 +
+ t=-
t=- t+
t+ ,
,解得t=
 .
.分析:(1)易证四边形ADCO为正方形,然后由正弦三角函数的定义、勾股定理求得线段OB与OA的数量关系,最后由梯形的面积公式求得OA、OB的长度.由待定系数法求得直线AB的解析式;
(2)由(1)中OA、OB的长度,利用勾股定理求得AB=10;然后利用三角函数的定义求得AF=5t、PF=4t;最后根据对顶角相等、余弦三角函数的定义求得y与t的函数关系式.定义域由y所表示的实际意义来确定;
(3)易证得∠EDF=45°.又因为∠ADF+∠CDE=45°,所以AF+CE=EF.
点评:本题考查了一次函数综合题.其中涉及到的知识点有勾股定理、解直角三角形、待定系数法求一次函数的解析式、梯形的面积公式等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF. ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.