题目内容
【题目】△ABC内接于⊙O,AC为⊙O的直径,∠A=60°,点D在AC上,连接BD作等边三角形BDE,连接OE.
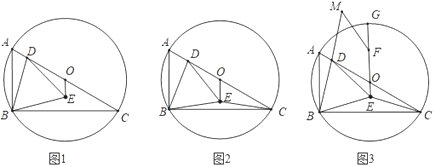
(1)如图1,求证:OE=AD;
(2)如图2,连接CE,求证:∠OCE=∠ABD;
(3)如图3,在(2)的条件下,延长EO交⊙O于点G,在OG上取点F,使OF=2OE,延长BD到点M使BD=DM,连接MF,若tan∠BMF=![]() ,OD=3,求线段CE的长.
,OD=3,求线段CE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)CE=![]() .
.
【解析】
(1)连接OB,证明△ABD≌△OBE,即可证出OE=AD.
(2)连接OB,证明△OCE≌△OBE,则∠OCE=∠OBE,由(1)的全等可知∠ABD=∠OBE,则∠OCE=∠ABD.
(3)过点M作AB的平行线交AC于点Q,过点D作DN垂直EG于点N,则△ADB≌△MQD,四边形MQOG为平行四边形,∠DMF=∠EDN,再结合特殊角度和已知的线段长度求出CE的长度即可.
解:(1)如图1所示,连接OB,
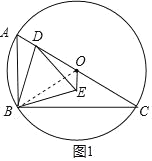
∵∠A=60°,OA=OB,
∴△AOB为等边三角形,
∴OA=OB=AB,∠A=∠ABO=∠AOB=60°,
∵△DBE为等边三角形,
∴DB=DE=BE,∠DBE=∠BDE=∠DEB=60°,
∴∠ABD=∠OBE,
∴△ADB≌△OBE(SAS),
∴OE=AD;
(2)如图2所示,
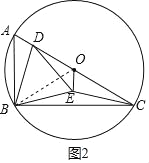
由(1)可知△ADB≌△OBE,
∴∠BOE=∠A=60°,∠ABD=∠OBE,
∵∠BOA=60°,
∴∠EOC=∠BOE =60°,
又∵OB=OC,OE=OE,
∴△BOE≌△COE(SAS),
∴∠OCE=∠OBE,
∴∠OCE=∠ABD;
(3)如图3所示,过点M作AB的平行线交AC于点Q,过点D作DN垂直EG于点N,
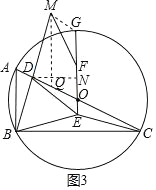
∵BD=DM,∠ADB=∠QDM,∠QMD=∠ABD,
∴△ADB≌△MQD(ASA),
∴AB=MQ,
∵∠A=60°,∠ABC=90°,
∴∠ACB=30°,
∴AB=![]() =AO=CO=OG,
=AO=CO=OG,
∴MQ=OG,
∵AB∥GO,
∴MQ∥GO,
∴四边形MQOG为平行四边形,
设AD为x,则OE=x,OF=2x,
∵OD=3,
∴OA=OG=3+x,GF=3﹣x,
∵DQ=AD=x,
∴OQ=MG=3﹣x,
∴MG=GF,
∵∠DOG=60°,
∴∠MGF=120°,
∴∠GMF=∠GFM=30°,
∵∠QMD=∠ABD=∠ODE,∠ODN=30°,
∴∠DMF=∠EDN,
∵OD=3,
∴ON=![]() ,DN=
,DN=![]() ,
,
∵tan∠BMF=![]() ,
,
∴tan∠NDE=![]() ,
,
∴ ,
,
解得x=1,
∴NE=![]() ,
,
∴DE=![]() ,
,
∴CE=![]() .
.
故答案为(1)证明见解析;(2)证明见解析;(3)CE=![]() .
.