题目内容
【题目】如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针防线旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.

【答案】(1) 105°;(2) 135°; (3)5或17;11或23
【解析】
(1)根据三角形的内角和定理列式计算即可得解;
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
解:(1)在△CEN中,
∠CEN=180°-∠DCN-∠MNO=180°-45°-30°=105°
(2)∵∠BON=∠N=30°,
∴MN∥CB,
∴∠CEN=180°-∠DCO=180°-45°=135°
(3)如图1,CD在AB上方时,设OM与CD相交于F,
∵CD∥MN,
∴∠OFD=∠M=60°,
在△ODF中,∠MOD=180°-∠D-∠OFD,
=180°-45°-60°,
=75°,
∴旋转角为75°,
t=75°÷15°=5秒;
CD在AB的下方时,设直线OM与CD相交于F,
∵CD∥MN,
∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转角为75°+180°=255°,
t=255°÷15°=17秒;
综上所述,第5或17秒时,边CD恰好与边MN平行;
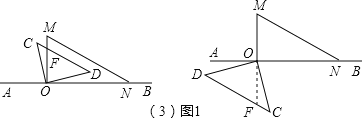
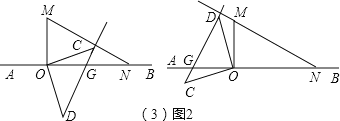
如图2,CD在OM的右边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGC=90°-∠MNO=90°-30°=60°,
∴∠CON=∠NGC-∠OCD=60°-45°=15°,
∴旋转角为180°-∠CON=180°-15°=165°,
t=165°÷15°=11秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°-∠MNO=90°-30°=60°,
∴∠AOC=∠NGD-∠C=60°-45°=15°,
∴旋转角为360°-∠AOC=360°-15°=345°,
t=345°÷15°=23秒,
综上所述,第11或23秒时,直线CD恰好与直线MN垂直.

 口算题天天练系列答案
口算题天天练系列答案