题目内容
【题目】如图,点A、B是数轴上的两个点,它们分别表示的数是![]() 和1. 点A与点B之间的距离表示为AB.
和1. 点A与点B之间的距离表示为AB.
(1)AB= .
(2)点P是数轴上A点右侧的一个动点,它表示的数是![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
(3)点C为6. 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:![]() 的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
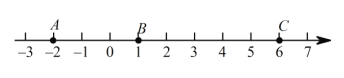
【答案】(1)3.(2)存在.x的值为3.(3)不变,为2.
【解析】
(1)根据非负数的性质和数轴上两点间距离即可求解;
(2)分两种情况讨论,根据数轴上两点间的距离公式列方程即可求解;
(3)先确定运动t秒后,A、B、C三点对应的数,再根据数轴上两点间的距离公式列方程即可求解.
解:(1)∵点A、B是数轴上的两个点,它们分别表示的数是![]() 和1
和1
∴A,B两点之间的距离是1-(-2)=3.
故答案为3.
(2)存在.理由如下:
①若P点在A、B之间,
x+2+1-x=7,此方程不成立;
②若P点在B点右侧,
x+2+x-1=7,解得x=3.
答:存在.x的值为3.
(3)![]() 的值不随运动时间t(秒)的变化而改变,为定值,是2.理由如下:
的值不随运动时间t(秒)的变化而改变,为定值,是2.理由如下:
运动t秒后,A点表示的数为-2-t,B点表示的数为1+2t,C点表示的数为6+5t.
所以AB=1+2t-(-2-t)=3+3t.
BC=6+5t-(1+2t)=5+3t.
所以BC-AB=5+3t-3-3t=2.

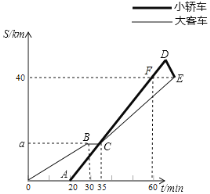
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?