题目内容
【题目】如图,大长方形是由四个小长方形拼成的,请根据此图填空:x2+(p+q)x+pq=x2+px+qx+pq=( )( ).
说理验证
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+()= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把x2+3x+2分解因式.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式分解因式:
(1)x2﹣7x+12; (2)(y2+y)2+7(y2+y)﹣18.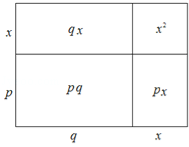
【答案】x+p x+q qx+pq x(x+p)+q(x+p) x+p x+q
(1)(x﹣3)(x﹣4) (2)(y2+y+9)(y+2)(y﹣1)
【解析】
试题由矩形的面积公式可以求得x2+px+qx+pq=(x+p)(x+q);
利用分组的方法可以先分组然后提公因式法可以分解因式为:x2+px+qx+pq=(x2+px)+(qx+pq)=x(x+p)+q(x+p)=(x+p)(x+q);
根据x2+(p+q)x+pq=(x+p)(x+q)的形式的运用,可以将一个二次三项式分解因式,从而求出结果.
解:由矩形的面积公式得:(x+p)(x+q);
根据分组分解法得:x(x+p)+q(x+p),(x+p)(x+q);
(1)原式=(x﹣3)(x﹣4)
(2)原式=(y2+y+9)(y2+y﹣2)
=(y2+y+9)(y+2)(y﹣1).
故答案为(x+p)(x+q);x(x+p)+q(x+p),(x+p)(x+q);

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目