Question

【题目】如图，⊙O是以原点为圆心，2为半径的圆，点P是直线y=﹣x+4上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为 ．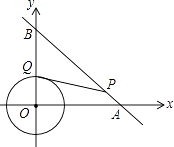

Answer 1

【答案】2
【解析】解：连结OP，OQ，作OH⊥AB于H，如图，
当x=0时，y=﹣x+4=4，则B（0，4）；当y=0时，﹣x+4=0，解得x=4，则A（4，0），
∵OA=OB，
∴△OAB为等腰直角三角形，
∴AB= OA=4 ，
∵OH⊥AB，
∴OH= AB=2 ，
∵PQ为⊙O的切线，
∴OQ⊥PQ，
在Rt△POQ中，PQ= = ，
∴当OP最小时，PQ最小，
而OP=OH时，OP最小，
∴切线长PQ的最小值= =2，
所以答案是：2．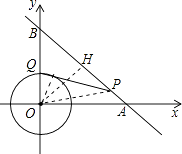

【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)．