题目内容
【题目】如图(1):△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F. 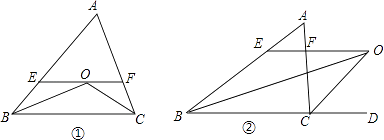
(1)EF与BE、CF之间有什么关系?(不证明)
(2)若△ABC中,∠B的平分线与三角外角∠ACD的平分线CO交于点O,过点O作OE∥BC交AB于E,交AC于F(图示),EF与BE,CF之间又有怎样的数量关系,并给予证明.
【答案】
(1)解:EF=BE+CF.
证明:∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EDB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE,
同理CF=OF,
∴EF=OE+OF=BE+CF,
即BE+CF=EF
(2)解:EF=BE﹣CF.
证明:∵BO平分∠ABC,
∴∠EBO=∠CBO,
∴BE=OE,
同理:CF=OF,
∴EF=OE﹣OF=BE﹣CF
【解析】(1)根据角平分线定义和平行线性质求出∠EOB=∠EBO,推出OE=BE,同理得出CF=OF,即可求出答案.(2)结合图形特点,根据(1)中规律,EF=BE﹣CF.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目