��Ŀ����
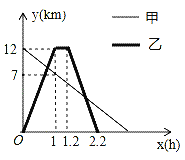
����Ŀ��ij��ֲ�������ŵ�������һ��С·����ͽ�������ų�������������ţ������ͬʱ�����������г��Ӳ�������ǰ�����ŵ������ź���Ϣ0.2Сʱ��Ȼ��ԭ·ԭ�����ٷ��ز��ţ�ͼ�����߷ֱ��ʾ�ס��ҵ����ŵľ���y��km�������ʱ��x��h��֮��ĺ�����ϵͼ����ͼ����Ϣ����������⣺
��1��������ŵľ���y��x֮��ĺ�����ϵʽ��
��2����ס��ҵ�һ������ʱ�����ŵľ��룮
��3����ס��ҵڶ���������ʱ�䣮
���𰸡���1��y=��5x+12��2��![]() ��3��
��3��![]()
��������
��1�����ݺ���ͼ���֪�㣨0��12���͵㣨1��7���ڼ�����Ϣǰ�����ŵ�·��y��km�������ʱ��x��h��֮��ĺ���ͼ���ϣ��Ӷ����Խ���⣻
��2�����ݺ���ͼ����Էֱ���ü��Ҹտ�ʼ���˶�Ӧ�ĺ�������ʽ�����������鼴����üס��ҵ�һ������ʱ�����ŵľ�����
��3�����ݺ���ͼ����Եõ������һ�μ�Ӧ�ĺ�������ʽ�����������鼴����üס��ҵڶ���������ʱ����
��1��������ŵľ���y��x֮��ĺ�����ϵʽΪy=kx+b��k��0����
����0��12������1��7������y=kx+b���ã�
![]() ����ã�
����ã�![]() ��
��
�������ŵľ���y��x֮��ĺ�����ϵʽΪy=��5x+12��
��2���赱0��x��1ʱ���ҵ����ŵľ���y��x֮��ĺ�����ϵʽΪy=ax��a��0����
����1��12������y=ax���ã�12=a��
����0��x��1ʱ���ҵ����ŵľ���y��x֮��ĺ�����ϵʽΪy=12x��
������������ϵʽ�ɷ����飬�ã�![]() ��
��
��ã� ��
��
���ס��ҵ�һ������ʱ�����ŵľ���Ϊ![]() km��
km��
��3���赱1.2��x��2.2ʱ���ҵ����ŵľ���y��x֮��ĺ�����ϵʽΪy=mx+n��m��0����
����1.2��12������2.2��0������y=mx+n���ã�
![]() ����ã�
����ã�![]() ��
��
����1.2��x��2.2ʱ���ҵ����ŵľ���y��x֮��ĺ�����ϵʽΪy=��12x+26.4��
������������ϵʽ�ɷ����飬�ã�![]() ��
��
��ã� ��
��
���ס��ҵڶ���������ʱ��Ϊ![]() h��
h��

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�