题目内容
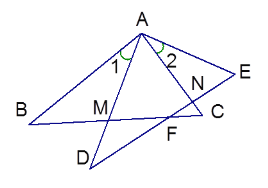
【题目】如图,已知CB//OA,∠C=∠A=104°,点E,F在BC上,OE平分∠COF,OB平分∠AOF
(1)求证:OC//AB;
(2)求∠EOB的度数;
(3)若平行移动AB,在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,请说明理由.

【答案】(1)见解析;(2)38°;(3)存在,57°
【解析】
(1)先根据两直线平行,同旁内角互补可知:∠C +∠COA =180°,再根据等角代换可得:∠A +∠COA =180°,然后根据平行线的判定定理可得OC∥AB;
(2)根据两直线平行,同旁内角互补求出∠COA,再根据角平分线的定义求出∠EOB=![]() ∠COA,代入数据即可;
∠COA,代入数据即可;
(3)先根据三角形内角和定理求出∠COE=∠BOA,从而得到OE、OF、OB是∠COA的四等分线,再利用三角形内角和定理列式计算即可.
证明:(1)∵ CB∥OA,
∴∠C +∠COA =180° ,
∵∠C=∠A,
∴∠A +∠COA =180°,
∴ OC∥AB;
(2)∵∠C=104°,
∴∠COA=180°-∠C =76° ,
∵ OE平分∠COF,OB平分∠AOF ,
∴∠COE=∠EOF,∠FOB=∠BOA,
∴∠EOB =∠EOF +∠FOB =![]() ∠COF +
∠COF +![]() ∠AOF =
∠AOF =![]() ∠COA =38° ;
∠COA =38° ;
(3)在△COE和△AOB中,
∵∠C =∠A,∠OEC =∠OBA,
∴∠COE =∠BOA ,
∴OE、OF、OB是∠COA的四等分线,
即 ∠COE =∠EOF =∠FOB =∠BOA,
∴∠COE =![]() ∠COA =
∠COA =![]() ×76°=19°,
×76°=19°,
∴∠OEC =180°-∠C -∠COE =180°-104°-19°= 57°,
答:存在某种情况使∠OEC=∠OBA,此时度数为 57°.

练习册系列答案
相关题目