题目内容
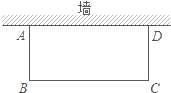
【题目】如图,点E在□ABCD内部,AF∥BE,DF∥CE.

(1)求证:△BCE≌△ADF;
(2)设□ABCD的面积为20,求四边形AEDF的面积.
【答案】(1)详见解析;(2)10.
【解析】
(1)根据ASA证明:△BCE≌△ADF;
(2)根据点E在ABCD内部,可知:S△BEC+S△AED=![]() SABCD,可得结论.
SABCD,可得结论.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,
∵AF∥BE,
∴∠EBA+∠BAF=180°,
∴∠CBE=∠DAF,
同理得∠BCE=∠ADF,
在△BCE和△ADF中,
∵ ,
,
∴△BCE≌△ADF(ASA);
(2)∵点E在ABCD内部,
∴S△BEC+S△AED=![]() SABCD,
SABCD,
由(1)知:△BCE≌△ADF,
∴S△BCE=S△ADF,
∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=![]() SABCD,
SABCD,
∵ABCD的面积为20,
∴四边形AEDF的面积为10.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目