Question

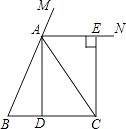
【题目】如图，在△ABC中，∠BAC＝120°，点D是BC的中点，且AD⊥AC，若AC＝3，则AB的长为________．

Answer 1

【答案】6

【解析】延长AD至E，使DE=AD，连接BE，由∠BAC=120°，∠DAC=90°，可得∠BAE =30°，根据SAS可证明△BED≌△CAD，从而可得∠BED=∠DAC=90°，BE=AC，再根据30度角所对的直角边等于斜边的一半即可求得AB的长.

延长AD至E，使DE=AD，连接BE，

∵∠BAC=120°，∠DAC=90°，

∴∠BAE=∠BAC-∠DAC=30°，

在△BED和△CAD中，

，

∴△BED≌△CAD（SAS），

∴∠BED=∠DAC=90°，BE=AC=3，

∴AB=2BE=6，

故答案为：6.