题目内容
【题目】乘法公式的探究和应用
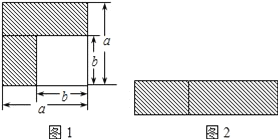
(1)如图1,可以求出阴影部分的面积是__.(写成两数平方差的形式)
(2)如图,若将阴影部分剪下来,重新拼成一个长方形,它的宽是__,长是__,面积是__.(写成多项式乘积的形式)
(3)比较左、右两图阴影部分的面积,可以得到乘法公式__.(用式子来表示)
(4)运用你所得到的公式,计算下列各题.
①![]() ②(2x﹣y+3)(2x﹣3+y)
②(2x﹣y+3)(2x﹣3+y)
【答案】(1)a2﹣b2;
(2)a﹣b;a+b;(a﹣b)(a+b);
(3)(a﹣b)(a+b)=a2﹣b2;
(4)①99![]() ;②4x2﹣9+6y﹣y2.
;②4x2﹣9+6y﹣y2.
【解析】(1)利用大正方形面积减去小正方形面积即可求出;(2)根据图形中长方形长与宽求出即可;(3)结合(1)(2)即可得出(a+b)(a-b)=a2-b2;
(4)10![]() ×9
×9![]() =(10+
=(10+![]() )(10﹣
)(10﹣![]() ),(2x-y+3)(2x-3+y)=[2x+(y-3)][2x-(y-3)],利用平方差公式进行运算即可,注意符合(a+b)(a-b)=a2-b2的形式才能运算.
),(2x-y+3)(2x-3+y)=[2x+(y-3)][2x-(y-3)],利用平方差公式进行运算即可,注意符合(a+b)(a-b)=a2-b2的形式才能运算.
解:(1)a2﹣b2;
(2)a﹣b;a+b;(a﹣b)(a+b);
(3)(a﹣b)(a+b)=a2﹣b2;
(4)①10![]() ×9
×9![]() =(10+
=(10+![]() )(10﹣
)(10﹣![]() )=100﹣
)=100﹣![]() =99
=99![]() ;
;
②(2x﹣y+3)(2x﹣3+y),
=[2x﹣(y﹣3)][2x+(y﹣3)],
=(2x)2﹣(y﹣3)2,
=4x2﹣(y2﹣6y+9),
=4x2﹣9+6y﹣y2.
“点睛”此题主要考查了平方差公式的几何背景,利用图形面积得出公式是近几年中考中考查重点,同学们应重点掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目