��Ŀ����
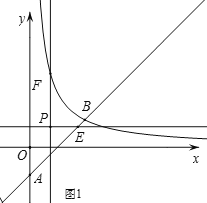
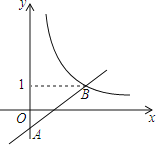
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��ax��a��aΪ��������ͼ����y���ཻ�ڵ�A���뺯��![]() ��x��0����ͼ���ཻ�ڵ�B��t��1����
��x��0����ͼ���ཻ�ڵ�B��t��1����
��1�����B�����꼰һ�κ����Ľ���ʽ��
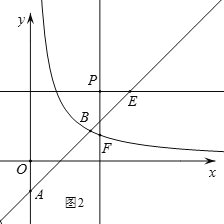
��2����P������Ϊ��m��m����m��0������P��PE��x�ᣬ��ֱ��AB�ڵ�E����PF��y�ᣬ������![]() ��x��0����ͼ���ڵ�F��
��x��0����ͼ���ڵ�F��
����m��2���Ƚ��߶�PE��PF�Ĵ�С��
��ֱ��д��ʹPE��PF��m��ȡֵ��Χ��
���𰸡���1��y��x��1����2����PE��PF����0��m��1��m��2��
��������
(1)��B(t��1)���뷴������������ʽ�������B�����꣬������B���������y��ax��a���ݴ���ϵ�����������һ�κ����Ľ���ʽ��
(2)������PE��x�ᣬ��ֱ��AB�ڵ�E��PF��y�ᣬ������![]() (x��0)��ͼ���ڵ�F�����ɵõ�PE��PF������m��2��PE��PF����m��1��PE��PF������PE��PF��������ͼ��õ�0��m��1��m��2��
(x��0)��ͼ���ڵ�F�����ɵõ�PE��PF������m��2��PE��PF����m��1��PE��PF������PE��PF��������ͼ��õ�0��m��1��m��2��
(1)������![]() (x��0)��ͼ����B(t��1)��
(x��0)��ͼ����B(t��1)��
��t��2��
��B(2��1)��
����y��ax��a�ã�1��2a��a��
��a��1��
��һ�κ����Ľ���ʽΪy��x��1��
(2)����m��2ʱ����P������Ϊ(2��2)��
����PE��x�ᣬ��ֱ��AB�ڵ�E��PF��y�ᣬ������![]() (x��0)��ͼ���ڵ�F��
(x��0)��ͼ���ڵ�F��
����y��2ʱ��2��x��1����x��3��
��PE��3��2��1��
��x��2ʱ��![]() ��1��
��1��
��PF��2��1��1��
��PE��PF��

�������ɵã���m��2��PE��PF��
��PE��m+1��m��1��
��![]() ��m��1����m��1��m����2(��ȥ)��
��m��1����m��1��m����2(��ȥ)��
����m��1��PE��PF��
��PE��PF��
����ͼ��ɵã�0��m��1��m��2��