题目内容
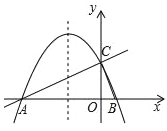
【题目】在如图所示的平面直角坐标系中，直线
与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c经过A，C两点，与x轴的另一交点为点B，其对称轴是
．
（1）求抛物线解析式．
（2）抛物线上是否存在点M（点m不与点C重合），使△MAB与△ABC的面积相等？若存在，求出点M的坐标；若不存在，请说明理由．
【答案】（1）
；（2）存在，M（﹣3，2）或（
，﹣2）或（
，﹣2）．
【解析】试题分析：（1）利用待定系数法进行求解即可得；
（2）设△ABM的边AB上的高为h，分情况讨论即可得.
试题解析：（1）y=
x+2，
当x=0时，y=2，
当y=0时，x=﹣4，
即A点的坐标为（﹣4，0），C点的坐标为（0，2），
∵抛物线y=ax2+bx+c经过A，C两点，与x轴的另一交点为点B，其对称轴是x=﹣
，
∴
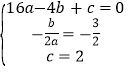，解得：a=﹣，b=﹣，c=2，
即抛物线解析式是y=﹣x2﹣x+2；
（2）存在，
理由是：设△ABM的边AB上的高为h，
∵点C的坐标为（0，2），
∴OC=2，
∵S△ABC=AB×OC=×AB×2，
∵△MAB与△ABC的面积相等，
∴AM×h=×AB×2，
∴h=2，
当点M在x轴的上方时，把y=2代入y=﹣x2﹣x+2得：x=0或x=﹣3，
∵M点和C点不重合，C的坐标为（0，2），
∴M的坐标为（﹣3，2）；
当点M在x轴的下方时，把y=﹣2代入y=﹣x2﹣x+2得：﹣2=﹣x2﹣x+2，
解得：x=或x=，
此时M的坐标为（，﹣2）或（，﹣2）；
综合上述：抛物线上存在点M（点M不与点C重合），使△MAB与△ABC的面积相等，此时点M的坐标是（﹣3，2）或（，﹣2）或（，﹣2）．
名校课堂系列答案
【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】
.
【解析】试题分析：
根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.
试题解析：
列表如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （1，2） | （1，3） | （1，4） |
2 | （2，1） | （2，2） | （2，3） | （2，4） |
3 | （3，1） | （3，2） | （3，3） | （3，4） |
4 | （4，1） | （4，2） | （4，3） | （4，4） |
由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，
∴P（两次摸到小球的数字之和等于4）=
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上BD处，另一部分在某一建筑的墙上CD处，分别测得其长度为9.6米和2米，求旗杆AB的高度．
