Question

【题目】如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．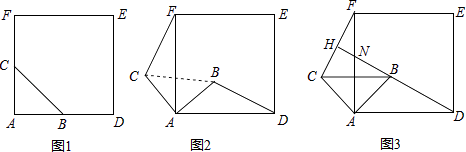
（1）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；
（2）当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．求证：BD⊥CF．

Answer 1

【答案】
（1）解：BD=CF．

理由如下：由题意得，∠CAF=∠BAD=θ，

在△CAF和△BAD中，

，

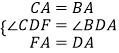∴△CAF≌△BAD（SAS），

∴BD=CF

（2）解：由（1）得△CAF≌△BAD，

∴∠CFA=∠BDA，

∵∠FNH=∠DNA，∠DNA+∠ADN=90°，

∴∠CFA+∠FNH=90°，

∴∠FHN=90°，即BD⊥CF

【解析】（1）根据旋转变换的性质和全等三角形的判定定理证明△CAF≌△BAD，证明结论；（2）根据全等三角形的性质、垂直的定义证明即可．
【考点精析】本题主要考查了等腰直角三角形和正方形的性质的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．