题目内容
【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（ 
，0），B（0，4），则点B2014的横坐标为 ． 
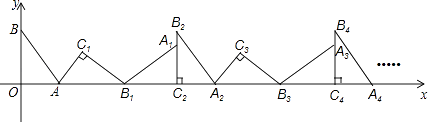
【答案】10070
【解析】解：由题意可得：∵AO= 
，BO=4，
∴AB= 
，
∴OA+AB1+B1C2= + +4=6+4=10，
∴B2的横坐标为：10，B4的横坐标为：2×10=20，
∴点B2014的横坐标为： 
×10=10070．
故答案为：10070．
首先利用勾股定理得出AB的长，进而得出三角形的周长，进而求出B2 ， B4的横坐标，进而得出变化规律，即可得出答案．
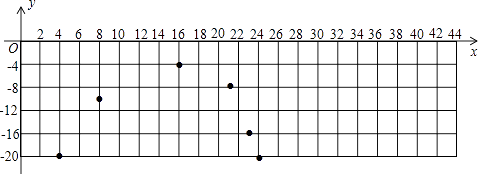
寒假天地重庆出版社系列答案
【题目】数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：当温度达到设定温度﹣20℃时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到﹣4℃时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至﹣20℃时，制冷再次停止，…，按照以上方式循环进行． 同学们记录了44min内15个时间点冷柜中的温度y（℃）随时间x（min）的变化情况，制成下表：
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
（1）通过分析发现，冷柜中的温度y是时间x的函数． ①当4≤x＜20时，写出一个符合表中数据的函数解析式；
②当20≤x＜24时，写出一个符合表中数据的函数解析式；
（2）a的值为；
（3）如图，在直角坐标系中，已描出了上表中部分数据对应的点，请描出剩余数据对应的点，并画出当4≤x≤44时温度y随时间x变化的函数图象． 