题目内容
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
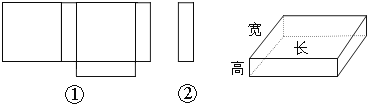
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
【答案】(1)8,
(2)四种可能,图形见详解
(3)128000 cm2
【解析】
(1)根据展开后的图形即可解题,(2)根据长方体的展开图的特点,进行画图,注意考虑周全.,(3)利用底面是正方形, 最长的一条棱是最短的一条棱的4倍,棱长的和是720cm,求出长宽高,即可解题.
解:(1)由展开图发现,小明一共剪开了8条棱,
故答案是8,
(2)如下图,四种可能,
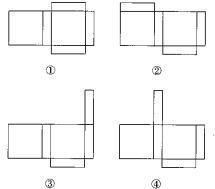
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长即高为acm,则长与宽相等为4acm.
∵长方体纸盒所有棱长的和是720cm,∴4(a+4a+4a)=720,解得a=20
这长方体纸盒的体积为20×80×80=128000cm2
故答案是8;四种情况;128000 cm2

 阅读快车系列答案
阅读快车系列答案【题目】城南中学九年级共有12个班,每班48名学生,学校对该年级学生数学学科学业水平测试成绩进行了抽样分析,请按要求回答下列问题:
【收集数据】
(1)要从九年级学生中抽取一个48人的样本,你认为以下抽样方法中最合理的是
________.①随机抽取一个班级的48名学生;②在九年级学生中随机抽取48名女学生;
③在九年级12个班中每班各随机抽取4名学生.
【整理数据】
(2)将抽取的48名学生的成绩进行分组,绘制成绩频数分布表和成绩分布扇形统计图如下.
请根据图表中数据填空:
①表中m的值为________;
② B类部分的圆心角度数为________°;
③估计C、D类学生大约一共有_________名.

九年级学生数学成绩频数分布表
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 24 |
|
B类(60~79) | 12 |
|
C类(40~59) | 8 | m |
D类(0~39) | 4 |
|
【分析数据】
(3)教育主管部们为了解学校学生成绩情况,将同层次的城南、城北两所中学的抽样数据进行对比分析,得到下表:
学校 | 平均数(分) | 方差 | A、B类的频率和 |
城南中学 | 71 | 358 | 0.75 |
城北中学 | 71 | 588 | 0.82 |
请你评价这两所学校学生数学学业水平测试的成绩,提出一个解释来支持你的观点.