题目内容
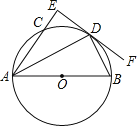
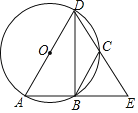
【题目】如图:AD是⊙O的直径,AD=12,点BC在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°,则以下判断中不正确的是( )
A.∠ADE=∠EB.劣弧AB的长为![]() π
π
C.点C为弧BD的中点D.BD平分∠ADE
【答案】D
【解析】
根据圆内接四边形的外角等于其内对角可得∠CBE=∠ADE,根据等边对等角得出∠CBE=∠E,等量代换即可得到∠ADE=∠E;根据圆内接四边形的外角等于其内对角可得∠A=∠BCE=70°,根据等边对等角以及三角形内角和定理求出∠AOB=40°,再根据弧长公式计算得出劣弧![]() 的长;
的长;
根据圆周角定理得出∠ACD=90°,即AC⊥DE,根据等角对等边得出AD=AE,根据等腰三角形三线合一的性质得出∠DAC=∠EAC,再根据圆周角定理得到点C为![]() 的中点;
的中点;
由DB⊥AE,而∠A≠∠E,得出BD不平分∠ADE.
∵ABCD是⊙O的内接四边形,
∴∠CBE=∠ADE,
∵CB=CE,
∴∠CBE=∠E,
∴∠ADE=∠E,故A正确;
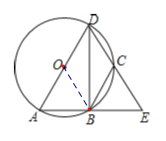
连接OB,
∵∠A=∠BCE=70°,OA=OB,
∴∠AOB=40°,
∴劣弧![]() 的长=
的长=![]() ,故B正确;
,故B正确;
∵AD是⊙O的直径,
∴∠ACD=90°,即AC⊥DE,
∵∠ADE=∠E,
∴AD=AE,
∴∠DAC=∠EAC,
∴点C为![]() 的中点,故C正确;
的中点,故C正确;
∵DB⊥AE,而∠A=70°≠∠E=![]() ,
,
∴BD不平分∠ADE,故D错误.
故选:D.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案【题目】据《北京晚报》介绍,自2009年故宫博物院年度接待观众首次突破1000万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆.特别是随着《我在故宫修文物》、《上新了,故宫》等一批电视文博节目的播出,社会上再次掀起故宫热.于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故宫的观众的年龄,整理并绘制了如下统计图表.
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x<30 | 80 | b |
30≤x<40 | a | 0.240 |
40≤x<50 | 35 | 0.175 |
50≤x<60 | 37 | c |
合计 | 200 | 1.000 |
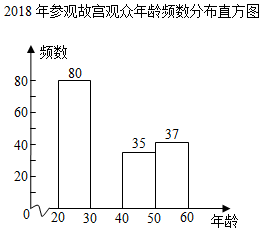
(1)求表中a,b,c的值;
(2)补全频数分布直方图;
(3)从数据上看,年轻观众(20≤x<40)已经成为参观故宫的主要群体.如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有 万人次.