ΧβΡΩΡΎ»ί
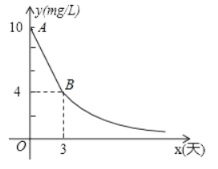
ΓΨΧβΡΩΓΩάΐΘΚάϊ”ΟΚ· ΐΆΦœσ«σΖΫ≥Χx2©¹2x©¹2ΘΫ0ΒΡ Β ΐΗυΘ®ΫαΙϊ±ΘΝτ–Γ ΐΒψΚσ“ΜΈΜΘ©Θ°
ΫβΘΚΜ≠≥ωΚ· ΐyΘΫx2©¹2x©¹2ΒΡΆΦœσΘ§Υϋ”κx÷αΒΡΙΪΙ≤ΒψΒΡΚαΉχ±ξ¥σ‘Φ «©¹0.7Θ§2.7Θ°Υυ“‘ΖΫ≥Χx2©¹2x©¹2ΘΫ0ΒΡ Β ΐΗυΈΣx1Γ÷©¹0.7Θ§x2Γ÷2.7Θ°Έ“Ο«ΜΙΩ…“‘Ά®Ιΐ≤ΜΕœΥθ–ΓΗυΥυ‘ΎΒΡΖΕΈßΙάΦΤ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυΘ°Γ≠Γ≠’β÷÷«σΗυΒΡΫϋΥΤ÷ΒΒΡΖΫΖ®“≤ ”Ο”ΎΗϋΗΏ¥ΈΒΡ“Μ‘ΣΖΫ≥ΧΘ°
ΗυΨίΡψΕ‘…œΟφΫΧ≤ΡΡΎ»ίΒΡ‘ΡΕΝ”κάμΫβΘ§ΫβΨωœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©άϊ”ΟΚ· ΐΆΦœσ»ΖΕ®≤ΜΒ» Ϋx2©¹4x+3ΘΦ0ΒΡΫβΦ· «ΓΓ ΓΓΘΜάϊ”ΟΚ· ΐΆΦœσ»ΖΕ®ΖΫ≥Χx2©¹4x+3ΘΫ![]() ΒΡΫβ «ΓΓ ΓΓΘ°
ΒΡΫβ «ΓΓ ΓΓΘ°
Θ®2Θ©ΈΣΧ÷¬έΙΊ”ΎxΒΡΖΫ≥Χ|x2©¹4x+3|ΘΫmΫβΒΡ«ιΩωΘ§Έ“Ο«Ω…άϊ”ΟΚ· ΐyΘΫ|x2©¹4x+3|ΒΡΆΦœσΫχ––―–ΨΩΘ°
ΔΌ«κ‘ΎΆχΗώΡΎΜ≠≥ωΚ· ΐyΘΫ|x2©¹4x+3|ΒΡΆΦœσΘΜ
ΔΎ»τΙΊ”ΎxΒΡΖΫ≥Χ|x2©¹4x+3|ΘΫm”–ΥΡΗω≤ΜœύΒ»ΒΡ Β ΐΫβΘ§‘ρmΒΡ»Γ÷ΒΖΕΈßΈΣΓΓ ΓΓΘΜ
Δέ»τΙΊ”ΎxΒΡΖΫ≥Χ|x2©¹4x+3|ΘΫm”–ΥΡΗω≤ΜœύΒ»ΒΡ Β ΐΫβx1Θ§x2Θ§x3Θ§x4Θ®x1ΘΦx2ΘΦx3ΘΦx4Θ©Θ§¬ζΉψx4©¹x3ΘΫx3©¹x2ΘΫx2©¹x1Θ§«σmΒΡ÷ΒΘ°


ΓΨ¥πΑΗΓΩ(1) 1ΘΦxΘΦ3Θ§xΘΫ4ΘΜ(2) ΔΌΦϊΫβΈωΘ§ΔΎ0ΘΦmΘΦ1Θ§ΔέmΘΫ0.8
ΓΨΫβΈωΓΩ
Μ≠≥ωΆΦœσΘ§ΗυΨίΧβ“βΆ®ΙΐΙέ≤λΩ…«σΫβΘ°
ΫβΘΚΘ®1Θ©x2©¹4x+3ΘΫ0”κx÷αΒΡΫΜΒψΈΣΘ®1Θ§0Θ©Θ§Θ®3Θ§0Θ©Θ§ΔέmΘΫ0.8
Γύx2©¹4x+3ΘΦ0ΒΡΫβΦ· «1ΘΦxΘΦ3Θ§
Μ≠≥ωΚ· ΐyΘΫx2©¹4x+3ΚΆΚ· ΐyΘΫ![]() ΒΡΆΦœσΘ§Ω…÷Σx2©¹4x+3ΘΫ
ΒΡΆΦœσΘ§Ω…÷Σx2©¹4x+3ΘΫ![]() ΒΡΫβΈΣxΘΫ4Θ§
ΒΡΫβΈΣxΘΫ4Θ§
Ι ¥πΑΗΈΣ1ΘΦxΘΦ3Θ§xΘΫ4ΘΜ
Θ®2Θ©ΔΌ»γΆΦΘΚ
ΔΎ»γΆΦΘΚΆ®ΙΐΙέ≤λΆΦœσΩ…÷ΣΘΚ
|x2©¹4x+3|ΘΫm”–ΥΡΗω≤ΜœύΒ»ΒΡ Β ΐΫβΘ§0ΘΦmΘΦ1ΘΜ
Ι ¥πΑΗΈΣ0ΘΦmΘΦ1ΘΜ
Δέ”…x4©¹x3ΘΫx3©¹x2ΘΫx2©¹x1Θ§Ω…ΒΟx2ΓΔx3 «x1x4ΒΡ»ΐΒ»Ζ÷ΒψΘ§
”…ΆΦΩ…÷ΣΘ§mΘΫ0.8 ±Θ§¬ζΉψx4©¹x3ΘΫx3©¹x2ΘΫx2©¹x1Θ°
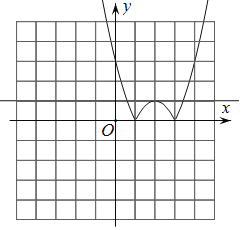
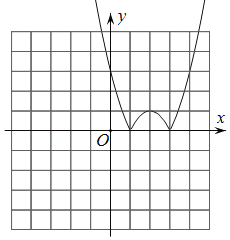

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ