题目内容
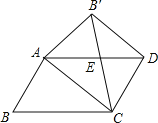
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,

求证:①△ABG≌△AFG;②BG=CG
【答案】①证明见解析;②证明见解析.
【解析】
①利用翻折变换对应边相等得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;
②根据题意可得DE=EF=2,在Rt△ECG中,设BG=FG=x,则CG=6-x.根据勾股定理得BG=3,CG=3,从而得BG=GC.
①∵四边形ABCD是正方形,
∴AB=AD=CD=6,∠B=∠D=90°,
由折叠的性质得:∠AFE=∠D=90°,AF=AD,EF=DE,
∴∠AFG=90°,AB=AF,
∴∠B=∠AFG=90°,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL);
②∵EF=DE=![]() CD=2,设BG=FG=x,则CG=6-x.
CD=2,设BG=FG=x,则CG=6-x.
在Rt△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,
解得:x=3.
∴BG=3,CG=6-3=3,
∴BG=CG.

【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民一户一表"生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 |
|
|
超过 |
|
|
(说明:每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)
已知小王家2018年7月用水![]() 吨,交水费
吨,交水费![]() 元.8月份用水
元.8月份用水![]() 吨,交水费
吨,交水费![]() 元.
元.
(1)求![]() 的值;
的值;
(2)如果小王家9月份上交水费![]() 元,则小王家这个月用水多少吨?
元,则小王家这个月用水多少吨?
(3)小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过![]() 吨,一共交水费
吨,一共交水费![]() 元,其中包含
元,其中包含![]() 元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)