��Ŀ����
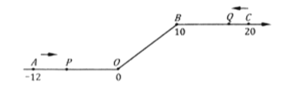
����Ŀ����ͼ����һ��������ԭ��![]() �͵�
�͵�![]() ������һ�£��õ�һ����������������ͼ�е�
������һ�£��õ�һ����������������ͼ�е�![]() ��ʾ-12����
��ʾ-12����![]() ��ʾ10����
��ʾ10����![]() ��ʾ20�����dzƵ�
��ʾ20�����dzƵ�![]() �͵�
�͵�![]() �����������32�����ȵ�λ������
�����������32�����ȵ�λ������![]() �ӵ�
�ӵ�![]() ��������2��λ/����ٶ��������������������������˶����ӵ�
��������2��λ/����ٶ��������������������������˶����ӵ�![]() �˶�����
�˶�����![]() �ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������
�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������![]() �ӵ�
�ӵ�![]() ��������1��λ/����ٶ�������������ĸ������˶����ӵ�
��������1��λ/����ٶ�������������ĸ������˶����ӵ�![]() �˶�����
�˶�����![]() �ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊ
�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊ![]() �룮��
�룮��
��1������![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ��Ҫʱ������룿
��Ҫʱ������룿
��2����![]() ��
��![]() �����ڵ�
�����ڵ�![]() �����������
�����������![]() ����������������ʾ�����Ƕ��٣�
����������������ʾ�����Ƕ��٣�
��3����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() ���������������ij�����
���������������ij�����![]() ��
��![]() ���������������ij�����ȣ�
���������������ij�����ȣ�
���𰸡���1��21����2��6����3����![]() ʱ��
ʱ��![]() ��
��
��������
��1������·�̳����ٶȵ���ʱ�䣬�ɵô𰸣�
��2����������ʱ![]() ��
��![]() �������߶�
�������߶�![]() �ϣ�����
�ϣ�����![]() =10���ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
=10���ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��3������PO��BQ��ʱ����ȣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
�⣺��1����P�˶�����Cʱ������ʱ��t��12��2��10��1��10��2��21���룩��
�𣺶���P�ӵ�A�˶���C����Ҫ21s ��
��2��������ɵ�![]() ��
��
![]() ��
��![]() �������߶�
�������߶�![]() ������
������
��![]() ��
��
��![]() ��
��
��![]() ���Ե�����Ϊ12-6=6;
���Ե�����Ϊ12-6=6;
��3������![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ʱ��
��ʱ��![]() ����
����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
����![]() ʱ��
ʱ��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�