Question

【题目】如图，正方形ABCD的边长为3，E、F分别是AB、CD上的点，且∠CFE=60°，将四边形BCFE沿EF翻折，得到B′C′FE，C′恰好落在AD边上，B′C′交AB于点G，则GE的长是（ ）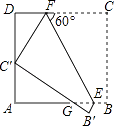

A.3 ﹣4
B.4 ﹣5
C.4﹣2
D.5﹣2

Answer 1

【答案】C
【解析】解：∵四边形ABCD是正方形，
∴∠A=∠B=∠C=∠D=90°，AB=AD=3，
由折叠的性质得：FC′=FC，∠C′FE=∠CFE=60°，∠FC′B′=∠C=90°，B′E=BE，∠B′=∠B=90°，
∴∠DFC′=60°，
∴∠DC′F=30°，
∴FC′=FC=2DF，
∵DF+CF=CD=3，
∴DF+2DF=3，
解得：DF=1，
∴DC′= DF= ，
则C′A=3﹣ ，AG= （3﹣ ），
设EB=x，
∵∠B′GE=∠AGC′=∠DC′F=30°，
∴GE=2x，
则 （3﹣ ）+3x=3，
解得：x=2﹣ ，
∴GE=4﹣2 ；
故选：C．
【考点精析】关于本题考查的正方形的性质和翻折变换（折叠问题），需要了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．