Question

【题目】如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．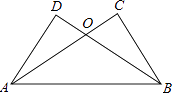

求证：
（1）BC=AD
（2）△OAB是等腰三角形．

Answer 1

【答案】
（1）

证明：∵AC⊥BC，BD⊥AD，

∴∠ADB=∠ACB=90°，

在Rt△ABC和Rt△BAD中，

∵ ，

∴Rt△ABC≌Rt△BAD（HL），

∴BC=AD，

（2）

证明：∵Rt△ABC≌Rt△BAD， ∴∠CAB=∠DBA，
∴OA=OB，
∴△OAB是等腰三角形．

【解析】（1）根据AC⊥BC，BD⊥AD，得出△ABC与△BAD是直角三角形，再根据AC=BD，AB=BA，得出Rt△ABC≌Rt△BAD，即可证出BC=AD，（2）根据Rt△ABC≌Rt△BAD，得出∠CAB=∠DBA，从而证出OA=OB，△OAB是等腰三角形．
【考点精析】掌握等腰三角形的判定是解答本题的根本，需要知道如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．