题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,
,![]() ,垂足分别是
,垂足分别是![]() 、
、![]() ,
,![]() .
.
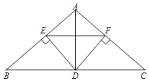
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,求证:四边形
,求证:四边形![]() 是正方形.
是正方形.
【答案】证明见解析
【解析】
(1)根据相似三角形的性质得到![]() =
=![]() ,根据AB=AC,得到AE=AF,利用HL定理证明;
,根据AB=AC,得到AE=AF,利用HL定理证明;
(2)根据等腰三角形的性质得到BC=2BD,得到BD=AD,根据正方形的判定定理即可证明.
(1)∵△AEF∽△ABC,∴![]() =
=![]() .
.
∵AB=AC,∴AE=AF.
∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.在Rt△AED和Rt△AFD中,∵![]() ,∴Rt△AED≌Rt△AFD;
,∴Rt△AED≌Rt△AFD;
(2)∵Rt△AED≌Rt△AFD,∴∠EAD=∠FAD.
∵AB=AC,∴AD⊥BC,BC=2BD.
∵BC=2AD,∴BD=AD.
∵AD⊥BC,∴∠ADB=90°,∴∠B=∠BAD=45°,∴∠BAC=2∠BAD=90°.
∵∠AED=∠AFD=90°,∴四边形AEDF是矩形.
∵AE=AF,∴矩形AEDF是正方形.

练习册系列答案
相关题目