题目内容
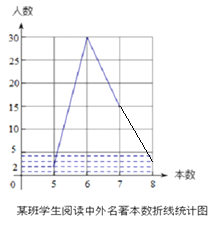
【题目】为响应“书香校园”号召，重庆一中在九年级学生中随机抽取某班学生对2016年全年阅读中外名著的情况进行调查，整理调查结果发现，每名学生阅读中外名著的本数，最少的有5本，最多的有8本，并根据调查结果绘制了如图所示的不完整的折线统计图和扇形统计图.
（1）该班学生共有 名，扇形统计图中阅读中外名著本数为7本所对应的扇形圆心角的度数是 度，并补全折线统计图；
（2）根据调查情况，班主任决定在阅读中外名著本数为5本和8本的学生中任选两名学生进行交流，请用树状图或表格求出这两名学生阅读的本数均为8本的概率.
【答案】（1）50,108，补全图见解析；
（2）树状图见解析，这两名学生阅读的本数均为8本的概率为
.
【解析】试题分析：（1）由折线图可知阅读6本名著的人数为30人，占60%，即可得出全班的人数为50人；用15除以50再乘360°得出阅读7本年名著所对应的圆心角的度数；再由50-2-30-15得出阅读8本名著的人数为3人；（2）根据题意画出图表，再根据概率公式即可得出答案．
试题解析：
解：（1）该班学生共有30÷60%=50名，
扇形统计图7本所对应的圆心角的度数为360°×
=108°
补全如图：
(2)分别用A，B表示阅读5本的学生，用C，D表示阅读8本的学生，
画树状图得：
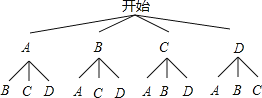
∵共有12种等可能的结果，抽到的两名学生都阅读了8本有2种结果
∴抽到的两名学生都阅读了8本的概率为： 
.
【题目】某学校欲招聘一名新教师，对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核，他们的各项得分（百分制）如下表所示：
应试者 | 面试成绩 | 笔试成绩 | 才艺 |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
（1）根据三项得分的平均分，从高到低确定应聘者的排名顺序；
（2）学校规定：笔试、面试、才艺得分分别不得低于80分、80分、70分，并按照60%、30%、10%的比例计入个人总分，请你说明谁会被录用？
