题目内容
【题目】某商店欲购进甲、乙两种商品，已知甲的进价是乙的进价的一半，进3件甲商品和1件乙商品恰好用200元．甲、乙两种商品的售价每件分别为80元、130元，该商店决定用不少于6710元且不超过6810元购进这两种商品共100件．
（1）求这两种商品的进价．
（2）该商店有几种进货方案？哪种进货方案可获得最大利润，最大利润是多少？
【答案】（1）商品的进价为40元，乙商品的进价为80元．
（2）有三种进货方案：
方案1，甲种商品30件，乙商品70件；
方案2，甲种商品31件，乙商品69件；
方案3，甲种商品32件，乙商品68件．
方案1可获得最大利润，最大=4700．
【解析】
（1）设甲商品的进价为x元，乙商品的进价为y元，就有
，3x+y=200，由这两个方程构成方程组求出其解即可．
（2）设购进甲种商品m件，则购进乙种商品（100﹣m）件，根据不少于6710元且不超过6810元购进这两种商品100的货款建立不等式，求出其值就可以得出进货方案，设利润为W元，根据利润=售价﹣进价建立解析式就可以求出结论．
解：（1）设甲商品的进价为x元，乙商品的进价为y元，由题意，得
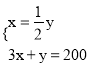，解得：
．
答：商品的进价为40元，乙商品的进价为80元．
（2）设购进甲种商品m件，则购进乙种商品（100﹣m）件，由题意，得
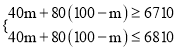，解得：
．
∵m为整数，∴m=30，31，32．
∴有三种进货方案：
方案1，甲种商品30件，乙商品70件；
方案2，甲种商品31件，乙商品69件；
方案3，甲种商品32件，乙商品68件．
设利润为W元，由题意，得
，
∵k=﹣10＜0，∴W随m的增大而减小．
∴m=30时，W最大=4700．
练习册系列答案
相关题目
