题目内容
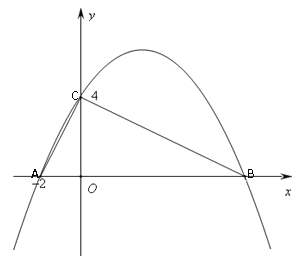
【题目】如图,在平面直角坐标系中,抛物线![]() 经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C坐标为(0,4).
经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C坐标为(0,4).
(1)求该抛物线的解析式.
(2)如果将线段OB绕原点O逆时针旋转60°到0D位置,那么点B的对应点D是否会落在该抛物线的对称轴上?请说明理由.
【答案】(1)![]() ;(2)点D不会落在该抛物线的对称轴上.理由见解析.
;(2)点D不会落在该抛物线的对称轴上.理由见解析.
【解析】试题分析:(1)首先证明△ACO∽△CBO,根据相似三角形的性质可得![]() ,然后可得B点坐标,再利用待定系数法求出抛物线解析式即可;
,然后可得B点坐标,再利用待定系数法求出抛物线解析式即可;
(2)根据抛物线解析式计算出对称轴,再根据等边三角形的判定可得△BOD是等边三角形,再根据等腰三角形三线合一的性质可得D点横坐标,进而可得答案.
试题解析:(1)由题意得:CO⊥AB,OA=2,OC=4
∵∠ACB=90°, CO⊥AB
∴∠ACO+∠BCO=90°,∠ACO+∠CAO=90°,∠AOC=∠COB=90°
∴∠BCO=∠CAO
∴△AOC∽△COB
∴![]()
∴![]() 解得 OB=8
解得 OB=8
∴点B坐标为(8,0)分
∵抛物线![]() 经过点A、B、C
经过点A、B、C
∴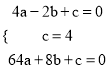
解得
∴该抛物线的解析式为![]() .
.
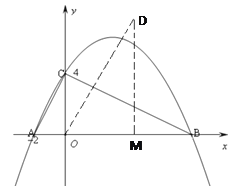
(2)点D不会落在该抛物线的对称轴上.
理由:作DM⊥x轴于点M,则在Rt△ODM中,OD=OB=8,∠DOM=60°
∴∠ODM=30°
∴OM=![]() .
.
∴点D的横坐标为4
又由(1)可知,该抛物线的对称轴是直线x=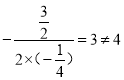
∴旋转后点B的对应点D不会落在该抛物线的对称轴上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目