题目内容
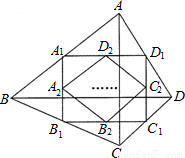
如图,四边形ABCD中,AC=a,BD=b,且AC丄BD,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是
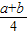
④四边形AnBnCnDn的面积是
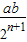 .
.
A.①②
B.②③
C.②③④
D.①②③④
【答案】分析:首先根据题意,找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律,然后对以下选项作出分析与判断:
①根据矩形的判定与性质作出判断;
②根据菱形的判定与性质作出判断;
③由四边形的周长公式:周长=边长之和,来计算四边形A5B5C5D5的周长;
④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积.
解答: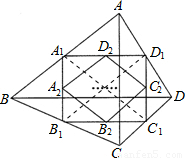 解:①连接A1C1,B1D1.
解:①连接A1C1,B1D1.
∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,∴四边形A1B1C1D1是矩形,
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
故本选项错误;
②由①知,四边形A2B2C2D2是菱形;
∴根据中位线定理知,四边形A4B4C4D4是菱形;
故本选项正确;
③根据中位线的性质易知,A5B5= A3B3=
A3B3= ×
× A1B1=
A1B1= ×
× ×
× AC,B5C5=
AC,B5C5= B3C3=
B3C3= ×
× B1C1=
B1C1= ×
× ×
× BD,
BD,
∴四边形A5B5C5D5的周长是2× (a+b)=
(a+b)=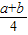 ;
;
故本选项正确;
④∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是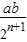 ;
;
故本选项正确;
综上所述,②③④正确.
故选C.
点评:本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半).解答此题时,需理清菱形、矩形与平行四边形的关系.
①根据矩形的判定与性质作出判断;
②根据菱形的判定与性质作出判断;
③由四边形的周长公式:周长=边长之和,来计算四边形A5B5C5D5的周长;
④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积.
解答:
 解:①连接A1C1,B1D1.
解:①连接A1C1,B1D1.∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,∴四边形A1B1C1D1是矩形,
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
故本选项错误;
②由①知,四边形A2B2C2D2是菱形;
∴根据中位线定理知,四边形A4B4C4D4是菱形;
故本选项正确;
③根据中位线的性质易知,A5B5=
 A3B3=
A3B3= ×
× A1B1=
A1B1= ×
× ×
× AC,B5C5=
AC,B5C5= B3C3=
B3C3= ×
× B1C1=
B1C1= ×
× ×
× BD,
BD,∴四边形A5B5C5D5的周长是2×
 (a+b)=
(a+b)=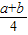 ;
;故本选项正确;
④∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是
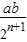 ;
;故本选项正确;
综上所述,②③④正确.
故选C.
点评:本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半).解答此题时,需理清菱形、矩形与平行四边形的关系.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.