ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ![]() Θ§œΏΕΈ
Θ§œΏΕΈ![]() ΓΔ
ΓΔ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() Θ§Ν§Ϋα
Θ§Ν§Ϋα![]() ΓΔ
ΓΔ![]() Θ§Έ“Ο«Α―–Έ»γΆΦ
Θ§Έ“Ο«Α―–Έ»γΆΦ![]() ΒΡΆΦ–Έ≥Τ÷°ΈΣΓΑ
ΒΡΆΦ–Έ≥Τ÷°ΈΣΓΑ![]() Γ±Ή÷–ΈΘ§»γΆΦ
Γ±Ή÷–ΈΘ§»γΆΦ![]() Θ§‘ΎΆΦ
Θ§‘ΎΆΦ![]() ΒΡΧθΦΰœ¬Θ§
ΒΡΧθΦΰœ¬Θ§![]() ΚΆ
ΚΆ![]() ΒΡΤΫΖ÷œΏ
ΒΡΤΫΖ÷œΏ![]() ΚΆ
ΚΆ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§≤Δ«“”κ
Θ§≤Δ«“”κ![]() ΓΔ
ΓΔ![]() Ζ÷±πœύΫΜ”Ύ
Ζ÷±πœύΫΜ”Ύ![]() ΓΔ
ΓΔ![]() Θ§ ‘Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ§ ‘Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
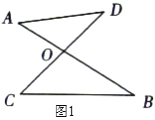
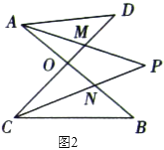
(1)‘ΎΆΦ![]() ÷–Θ§«κ÷±Ϋ”–¥≥ω
÷–Θ§«κ÷±Ϋ”–¥≥ω![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘΚ__________
÷°ΦδΒΡ ΐΝΩΙΊœΒΘΚ__________
(2)Ή–œΗΙέ≤λΘ§‘ΎΆΦ![]() ÷–ΓΑ
÷–ΓΑ![]() Γ±Ή÷–ΈΒΡΗω ΐΘΚ______ΗωΘΜ
Γ±Ή÷–ΈΒΡΗω ΐΘΚ______ΗωΘΜ
(3)ΆΦ![]() ÷–Θ§Β±
÷–Θ§Β±![]() Ε»Θ§
Ε»Θ§![]() Ε» ±Θ§«σ
Ε» ±Θ§«σ![]() ΒΡΕ» ΐ.
ΒΡΕ» ΐ.
(4)ΆΦ![]() ÷–
÷–![]() ΚΆ
ΚΆ![]() ΈΣ»Έ“βΫ« ±Θ§ΤδΥϋΧθΦΰ≤Μ±δΘ§ ‘Έ
ΈΣ»Έ“βΫ« ±Θ§ΤδΥϋΧθΦΰ≤Μ±δΘ§ ‘Έ ![]() ”κ
”κ![]() ΓΔ
ΓΔ![]() ÷°Φδ¥φ‘ΎΉ≈‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ(÷±Ϋ”–¥≥ωΫαΙϊΘ§≤Μ±Ί÷ΛΟς)
÷°Φδ¥φ‘ΎΉ≈‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ(÷±Ϋ”–¥≥ωΫαΙϊΘ§≤Μ±Ί÷ΛΟς)
ΓΨ¥πΑΗΓΩ(1)![]() ΘΜ(2)6ΘΜ(3)
ΘΜ(2)6ΘΜ(3)![]() ΘΜ(4)
ΘΜ(4)![]() .
.
ΓΨΫβΈωΓΩ
(1)ΗυΨί»ΐΫ«–ΈΒΡΡΎΫ«ΚΆΕ®άμ“‘ΦΑΕ‘ΕΞΫ«œύΒ»Ν– Ϋ’ϊάμΦ¥Ω…ΒΟΫβΘΜ
(2)ΗυΨίΕΞΒψ’“≥ωΓΑ8Ή÷–ΈΓ±ΒΡΗω ΐΦ¥Ω…ΘΜ
(3)ΗυΨίΫ«ΤΫΖ÷œΏΒΡΕ®“εΩ…ΒΟΓœ1=Γœ2Θ§Γœ3=Γœ4Θ§ΗυΨίΓΑ![]() Ή÷–ΈΓ±–‘÷ Ω…ΒΟΘΚ
Ή÷–ΈΓ±–‘÷ Ω…ΒΟΘΚ![]() ΔΌΘ§
ΔΌΘ§![]() ΔΎΘ§ΦΧΕχΩ…ΒΟ
ΔΎΘ§ΦΧΕχΩ…ΒΟ![]() Θ§¥ζ»κœύΙΊ ΐΨίΦ¥Ω…«σΒΟ¥πΑΗΘΜ
Θ§¥ζ»κœύΙΊ ΐΨίΦ¥Ω…«σΒΟ¥πΑΗΘΜ
(4)ΗυΨί(3)ΒΡΆΤΒΦΖΫΖ®Φ¥Ω…«σΒΟΫα¬έ.
(1)ΗυΨί»ΐΫ«–ΈΒΡΡΎΫ«ΚΆΕ®άμΘ§ΓœAOD+ΓœA+ΓœD=180ΓψΘ§ΓœBOC+ΓœB+ΓœC=180ΓψΘ§
ΓΏΓœAOD=ΓœBOC(Ε‘ΕΞΫ«œύΒ»)Θ§
Γύ![]() Θ§
Θ§
Ι ¥πΑΗΈΣΘΚΓœA+ΓœD=ΓœB+ΓœCΘΜ
(2) “‘ΒψOΈΣΕΞΒψΒΡΓΑ8Ή÷–ΈΓ±”–ΓςAODΚΆΓςBOCΘ§ΓςAOMΚΆΓςCONΘ§ΓςAODΚΆΓςCONΘ§ΓςAOMΚΆΓςBOCΘ§
“‘ΒψMΈΣΕΞΒψΒΡΓΑ8Ή÷–ΈΓ±”–ΓςADMΚΆΓςCMPΘ§
“‘ΒψNΈΣΕΞΒψΒΡΓΑ8Ή÷–ΈΓ±”–ΓςANPΚΆΓςBCNΘ§
Ι≤”–6ΗωΘ§
Ι ¥πΑΗΈΣΘΚ6ΘΜ
(3)»γΆΦ2Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§
ΓύΓœ1=Γœ2Θ§Γœ3=Γœ4Θ§
ΗυΨίΓΑ![]() Ή÷–ΈΓ±–‘÷ Ω…ΒΟΘΚ
Ή÷–ΈΓ±–‘÷ Ω…ΒΟΘΚ
![]() ΔΌΘ§
ΔΌΘ§
![]() ΔΎΘ§
ΔΎΘ§
”…ΔΌ![]() ΔΎΒΟΘ§
ΔΎΒΟΘ§
![]() Θ§
Θ§
![]() Θ§
Θ§
”÷![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() ΘΜ
ΘΜ
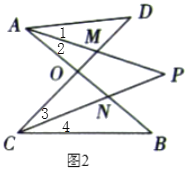
(4)![]() Θ§άμ”…»γœ¬ΘΚ
Θ§άμ”…»γœ¬ΘΚ
»γΆΦ2Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§
ΓύΓœ1=Γœ2Θ§Γœ3=Γœ4Θ§
ΗυΨίΓΑ![]() Ή÷–ΈΓ±–‘÷ Ω…ΒΟΘΚ
Ή÷–ΈΓ±–‘÷ Ω…ΒΟΘΚ
![]() ΔΌΘ§
ΔΌΘ§
![]() ΔΎΘ§
ΔΎΘ§
”…ΔΌ![]() ΔΎΒΟΘ§
ΔΎΒΟΘ§
![]() Θ§
Θ§
Φ¥![]() .
.

 ΉΏΫχΈΡ―‘ΈΡœΒΝ–¥πΑΗ
ΉΏΫχΈΡ―‘ΈΡœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥÷–―ßΉΦ±ΗΑα»κ–¬–Θ…α,‘Ύ«®»κ–¬–Θ…α«ΑΨΆΗΟ–Θ300Οϊ―ß…ζ»γΚΈΒΫ–ΘΈ ΧβΫχ––ΝΥ“Μ¥ΈΒς≤ι,≤ΔΒΟΒΫ»γœ¬ ΐΨί:
≤Ϋ–– | 65»Υ |
ΤοΉ‘––≥Β | 100»Υ |
ΉχΙΪΙ≤Τϊ≥Β | 125»Υ |
ΤδΥϊ | 10»Υ |
ΓΓΓΓ
ΫΪ…œΟφΒΡ ΐΨίΖ÷±π÷Τ≥……»–ΈΆ≥ΦΤΆΦΚΆΧθ–ΈΆ≥ΦΤΆΦ.