题目内容
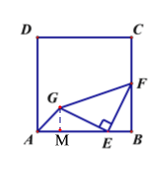
【题目】如图,正方形ABCD 的边长为4,E 为AB 上一点,且AE=3 ,F 为BC 边上的一个动点,连接EF ,以EF 为边向左侧作等腰直角三角形FEG ,EG=EF,∠GEF=90°,连接AG ,则AG 的最小值为________________.

【答案】1
【解析】
过点G作GM⊥AB于点M,由AAS可证:MGE BEF,得GM=1,即:点G与直线AB的距离为1,进而即可得到答案.
过点G作GM⊥AB于点M,
∵以EF 为边向左侧作等腰直角三角形FEG ,EG=EF,∠GEF=90°,
∴∠MGE+∠MEG=∠MEG+∠BEF=90°,
∴∠MGE=∠BEF,
∵正方形ABCD中,∠B=∠GME=90°,
∴MGE BEF(AAS),
∴GM=EB=AB-AE=4-3=1,
∴点G与直线AB的距离为1,
∴当AG⊥AB时,AG 有最小值,最小值为1.
故答案是:1.

练习册系列答案
相关题目