题目内容
【题目】在购买某场足球门票时,设购买门票数为x(张),费用为y(元).现有两种购买方案:
方案一:若单位费助广告费10000元,则该单位所购门票的价格为每张60元;(总费用=广告赞助费+门票费)
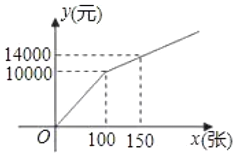
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0![]() x
x![]() 100时,y与x的函数关系式为 ;
100时,y与x的函数关系式为 ;
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由.
【答案】(1)y=60x+10000,y=100x,y=80x+2000;(2)当购买100张以上400张以下时,选择方案二,当购买400张以上时,选择方案一,当购买400张时,两个方案皆可,理由见详解.
【解析】
(1)根据题意可直接写出方案一的函数解析式,根据待定系数法求出方案二的函数解析式即可;
(2)根据题意,列出关于x的一元一次方程和一元一次不等式,分情况讨论即可.
(1)∵方案一中,总费用=广告赞助费+门票费,
∴y=60x+10000,
在方案二中,当0≤x≤100时,设函数关系式为:y=ax,
把(100,10000)代入上式得:10000=100a,解得:a=100,
∴y=100x,
当x>100时,设函数关系式为:y=kx+b,
把 (100,10000)和(150,14000)代入上式得:![]() ,解得:
,解得:![]() ,
,
∴y与x的函数关系式:y=80x+2000,
故答案是:y=60x+10000,y=100x,y=80x+2000;
(2)∵购买本场足球赛超过100张,
∴当60x+10000=80x+2000时,解得:x=400,
当60x+10000>80x+2000时,解得:x<400,
当60x+10000<80x+2000时,解得:x>400,
∴当购买100张以上400张以下时,选择方案二,当购买400张以上时,选择方案一,当购买400张时,两个方案皆可.

 高中必刷题系列答案
高中必刷题系列答案【题目】某中学准备搬入新校舍,在迁入新校舍前就该校300名学生如何到校问题进行了一次调查,并得到如下数据:
步行 | 65人 |
骑自行车 | 100人 |
坐公共汽车 | 125人 |
其他 | 10人 |
将上面的数据分别制成扇形统计图和条形统计图.