题目内容
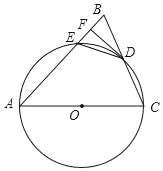
【题目】在等腰Rt△ABC中,CA=BA,∠CAB=90°,点M是AB上一点,
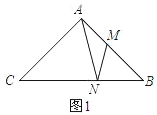
(1)点N为BC上一点,满足∠CNM=∠ANB.
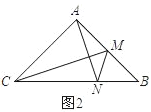
①如图1,求证:![]() ;②如图2,若点M是AB的中点,连接CM,求
;②如图2,若点M是AB的中点,连接CM,求![]() 的值;
的值;
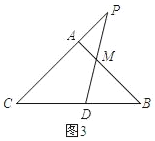
(2)如图3,若AM=1,BM=2,点P为射线CA(除点C外)上一个动点,直线PM交射线CB于点D,猜测△CPD面积是否有最小值,若有,请求出最小值:若没有,请说明理由.
【答案】(1)①见解析,②![]() ;(2)4.
;(2)4.
【解析】分析:
(1)①由已知条件易得∠B=∠C,∠BNM=∠CAN,从而可得△BNM∽△CNA,由此可得BM:CA=BN:CN结合CA=AB即可得到所求结论;
②如下图2,过点B作BH⊥BA交AN的延长线于点H,则结合已知条件易得△BMN≌△BHN,由此可得BH=BM=AM,从而可得△ACM≌△BAH,由此可得CM=AH=AN+NH=AN+NM,从而可得![]() ,结合由①中△BNM∽△CAN可得的:MN:AN=MB:AC=1:2即可求得所求比值;
,结合由①中△BNM∽△CAN可得的:MN:AN=MB:AC=1:2即可求得所求比值;
(2)如下图3,设点M是PD的中点,过点M作直线P′D′与射线CA,CB分别交于点P′,D′,则M不是P′D′中点,此时存在MD′>MP′或MD′<MP′两种情况,在两种情况下,分别证明S△P′CD′>S△PCD即可说明当点M是PD中点时,△PCD的面积最小,然后,如下图4,过点D作DH⊥AB于点H,证得△DHM≌△PAM,进一步证得△DBM和△PCD此时是等腰直角三角形,这样结合题目中的已知数量即可求得此时△PCD的面积了.
详解:
(1)① ∵CA=BA,∠CAB=90°,
∴∠C=∠B=45°,
∵∠CNM=∠ANB,
∴∠CNM﹣∠ANM=∠ANB﹣∠ANM,
∴∠ANC=∠BNM,
∴△CNA∽△BNM,
∴![]() ,
,
∵CA=BA,
∴![]() ;
;
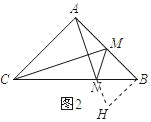
② 作BH⊥BA交AN的延长线于H,
∵ 在△BMN和△BHN中,
∠MBN=∠HBN=45°,BN=BN,∠MNB=∠HNB,
∴△BMN≌△BHN,
则△ACM≌△BAH,
∴CM=AH=AN+NH=AN+NM,
由①△CNA∽△BNM,点M是AB的中点,
∴![]() =2,
=2,
∴![]() =
=![]() ;
;
(2)设点M是PD中点,过点M作直线P′D′与射线CA,CB分别交于点P′,D′,
则点M不是P′D′的中点,当MD′>MP′时,在MD′上截取ME=MP′,连接DE,
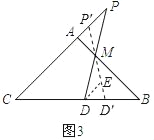
则△MPP′≌△MDE,
∴S△P′CD′>S四边形P′CDE=S△PCD,
当 MD′<MP′时,同理可得,S△P′CD′>S△PCD,
∴当点M是PD中点,△CPD面积的最小.
如图4,作DH⊥AB于H,
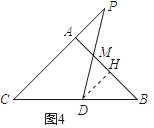
则△DHM≌△PAM.
∴AM=1,MH=1,BH=1,
∴△MDB是等腰直角三角形,
∴DH=BH=AP=1,∠PDC=90°,
∴△PCD是等腰直角三角形,CP=3+1=4,
∴△PCD的面积=4.

【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g) | ﹣5 | ﹣2 | 0 | 1 | 3 | 6 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)计算这批样品的平均重量,判断它比标准重量重还是轻多少?
(2)若标准重量为450克,则这批样品的总重量是多少?
(3)若这种食品的合格标准为450±5克,则这批样品的合格率为 (直接填写答案)
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如下图所示:

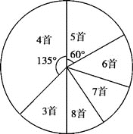
大赛结束后一个月,再次调查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人 数 | 10 | 10 | 15 | m | 25 | 20 |
请根据调查的信息
(1)本次调查抽取了多少名学生?
(2)补全条形统计图,在扇形统计图中,“6首”的圆心角为 度;
(3)表格中m的值为 ;
(4)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;