题目内容
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.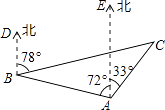
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】
(1)
解:∵BD∥AE,
∴∠DBA+∠BAE=180°,
∴∠DBA=180°﹣72°=108°,
∴∠ABC=108°﹣78°=30°
(2)
解:作AH⊥BC,垂足为H,
∴∠C=180°﹣72°﹣33°﹣30°=45°,
∵∠ABC=30°,
∴AH= ![]() AB=12,
AB=12,
∵sinC= ![]() ,
,
∴AC= ![]() =
= ![]() =12
=12 ![]() .
.
则A到出事地点的时间是: ![]() ≈
≈ ![]() ≈0.57小时.
≈0.57小时.
答:约0.57小时能到达出事地点.

【解析】(1)根据两直线平行,同旁内角互补,即可得到∠DBA的度数,则∠ABC即可求得;(2)作AH⊥BC于点H,分别在直角△ABH和直角△ACH中,利用三角函数求得BH和CH的长,则BC即可求得,进而求得时间.
【考点精析】掌握关于方向角问题是解答本题的根本,需要知道指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.

练习册系列答案
相关题目