题目内容
问题:如图(12),在菱形 和菱形
和菱形 中,点
中,点 在同一条直线上,
在同一条直线上, 是线段
是线段 的中点,连结
的中点,连结 .探究
.探究 与
与 的位置关系及
的位置关系及 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长 交
交 于点
于点 ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.

请你参考小聪同学的思路,探究并解决下列问题:
小题1:若图(12)中 ,写出线段
,写出线段 与
与 的位置关系及
的位置关系及 的值,并说明理由;
的值,并说明理由;
小题2:将图(12)中的菱形 绕点
绕点 顺时针旋转,使菱形
顺时针旋转,使菱形 的对角线
的对角线 恰好与菱形
恰好与菱形 的边
的边 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
小题3:若图(12)中 ,将菱形
,将菱形 绕点
绕点 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出 的值(用含
的值(用含 的式子表示).
的式子表示).
解:(1)线段 与
与 的位置关系是 ;
的位置关系是 ; .
.
 和菱形
和菱形 中,点
中,点 在同一条直线上,
在同一条直线上, 是线段
是线段 的中点,连结
的中点,连结 .探究
.探究 与
与 的位置关系及
的位置关系及 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长 交
交 于点
于点 ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
小题1:若图(12)中
 ,写出线段
,写出线段 与
与 的位置关系及
的位置关系及 的值,并说明理由;
的值,并说明理由;小题2:将图(12)中的菱形
 绕点
绕点 顺时针旋转,使菱形
顺时针旋转,使菱形 的对角线
的对角线 恰好与菱形
恰好与菱形 的边
的边 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.小题3:若图(12)中
 ,将菱形
,将菱形 绕点
绕点 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出 的值(用含
的值(用含 的式子表示).
的式子表示).解:(1)线段
 与
与 的位置关系是 ;
的位置关系是 ; .
.小题1:线段
 与
与 的位置关系是
的位置关系是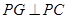 ,
, ;………………………………4分
;………………………………4分小题2:猜想:(1)中的结论没有发生变化. ………………………………………5分
简证:延长GP交AD于点H,连结CH,CG.
易证△GFP≌△HDP(AAS).
∴GP=HP,GF=HD.
又易证△HDC≌△GBC
∴CH=CG,∠DCH=∠BCG.
∵∠DCH =120°.
∵CH=CG,GP=HP.
∴ GP⊥PC,∠GCP=∠HCP=60° ,则
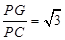 .……………………10分
.……………………10分小题3:
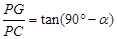 ………………………………………………………12分
………………………………………………………12分(1).按照小聪的思路作完图之后,GF平行于AB平行于CD,P又是中点,∠HDP=∠GFP,∠HPD=∠GPE,P为中点,所以△HDP全等于△GFP,这样DH=GF,所以CH=CG,则有等腰△CHG,有P为HG中点,所以PC⊥PG,因为菱形ABCD∠ABC=60°度所以∠DCB="120" °CP为角平分线,∠ PCG=60°PG:PC="√3"
(2)结论不变。延长CP交AB于M,连CG,MG。因为P是DF重点,所以DC=MF,CP=MP。有MF=CD=BC。考虑△CGB与△MGF,有BC=MF,∠CBG=∠MFG=60°,BG=GF,因此两三角形全等。从而CG=MG,∠CGB=∠MGF。因为∠CGB=∠CGM+∠GMB=∠MGF=∠FGB+∠BGM,因此∠CGM=∠FGB=60°,又有CG=GM,所以△CGM是等边三角形,且P是CM中点,从而原结论在此也成立。
(3)延长CP至M,使PM=PC,连MF交BG于N。易知CD‖MF‖AB。与上小问类似,可知MF=DC=BC,FG=BG。因为MF‖AB,有∠ABG=∠MNG,而∠ABG=∠ABC+∠CBG,∠MNG=∠BGF+∠GFM。因为∠ABC=∠BEF=∠BGF,所以∠CBG=∠MFG。又有BG=FG,MF=BC,所以△CBG与△MFG全等。因此与上小问类似,有CG=MG,∠CGM=∠FGB=2a。因此∠CGP=a且PG⊥PC,因此PG:PC=cot(a).
(2)结论不变。延长CP交AB于M,连CG,MG。因为P是DF重点,所以DC=MF,CP=MP。有MF=CD=BC。考虑△CGB与△MGF,有BC=MF,∠CBG=∠MFG=60°,BG=GF,因此两三角形全等。从而CG=MG,∠CGB=∠MGF。因为∠CGB=∠CGM+∠GMB=∠MGF=∠FGB+∠BGM,因此∠CGM=∠FGB=60°,又有CG=GM,所以△CGM是等边三角形,且P是CM中点,从而原结论在此也成立。
(3)延长CP至M,使PM=PC,连MF交BG于N。易知CD‖MF‖AB。与上小问类似,可知MF=DC=BC,FG=BG。因为MF‖AB,有∠ABG=∠MNG,而∠ABG=∠ABC+∠CBG,∠MNG=∠BGF+∠GFM。因为∠ABC=∠BEF=∠BGF,所以∠CBG=∠MFG。又有BG=FG,MF=BC,所以△CBG与△MFG全等。因此与上小问类似,有CG=MG,∠CGM=∠FGB=2a。因此∠CGP=a且PG⊥PC,因此PG:PC=cot(a).

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目

 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示): ;
; ,
, 的中点
的中点 ,
, ,连接
,连接 ;
; 长为半径画弧,交
长为半径画弧,交 ;
; ⊥
⊥ 。
。 为黄金矩形。
为黄金矩形。

 -
-
 -
-
 -4.
-4. -
- .
.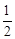 CD,CF=
CD,CF=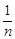 CD,CF=
CD,CF=

 = ▲ .
= ▲ .