题目内容
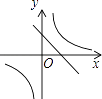
【题目】一次函数y=﹣ ![]() x+b(b为常数)的图象与x轴交于点A(2,0),与y轴交于点B,与反比例函数y=
x+b(b为常数)的图象与x轴交于点A(2,0),与y轴交于点B,与反比例函数y= ![]() 的图象交于点C(﹣2,m).
的图象交于点C(﹣2,m).
(1)求点C的坐标及反比例函数的表达式;
(2)过点C的直线与y轴交于点D,且S△CBD:S△BOC=2:1,求点D的坐标.
【答案】
(1)解:∵把点A(2,0)代入y=﹣ ![]() x+b得:b=1,
x+b得:b=1,
∴y=﹣ ![]() x+1,
x+1,
把点C(﹣2,m)代入y=﹣ ![]() x+1,解得m=2,
x+1,解得m=2,
∴C的坐标为(﹣2,2),
把C的坐标代入y= ![]() 得:k=﹣4,
得:k=﹣4,
∴反比例函数的表达式为y=﹣ ![]()
(2)解:∵B是y=﹣ ![]() x+1和y轴的交点,
x+1和y轴的交点,

∴B(0,1),
∵C(﹣2,2),
∴OB=1,
在△BOC中,OB边上的高为:2
∴S△BOC= ![]() =1,
=1,
∵过点C的直线与y轴交于点D,且S△CBD:S△BOC=2:1,
∴S△CBD=2,
设D的坐标为(0,m),
∴BD=|m﹣1|,
在△BDC中,BD边上的高为:2
∴ ![]() ×BD×2=2,
×BD×2=2,
∴BD=2,
∴m﹣1=±2
∴D点的坐标为(0,3)或(0,﹣1).
【解析】(1)把A点坐标代入y=﹣ ![]() x+b,求出b的值,再将C点的坐标代入求得的直线解析式,得到C点的坐标,再将C点的坐标代入双曲线的解析式即可;(2)求出B点的坐标,得到OB的长度,进而得出△BOC的面积,由过点C的直线与y轴交于点D,且S△CBD:S△BOC=2:1,得出S△CBD=2,设D的坐标为(0,m)得出BD=|m﹣1|,根据面积法得出BD的长度,进而找到D点的坐标。
x+b,求出b的值,再将C点的坐标代入求得的直线解析式,得到C点的坐标,再将C点的坐标代入双曲线的解析式即可;(2)求出B点的坐标,得到OB的长度,进而得出△BOC的面积,由过点C的直线与y轴交于点D,且S△CBD:S△BOC=2:1,得出S△CBD=2,设D的坐标为(0,m)得出BD=|m﹣1|,根据面积法得出BD的长度,进而找到D点的坐标。
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.

 考前必练系列答案
考前必练系列答案【题目】某公司计划开发![]() 、
、![]() 两种户型楼盘,设
两种户型楼盘,设![]() 户型
户型![]() 套,
套,![]() 户型
户型![]() 套,且两种户型的函数关系满足
套,且两种户型的函数关系满足![]() ,经市场调研,每套户型的成本价和预售价如下表所示:
,经市场调研,每套户型的成本价和预售价如下表所示:
楼盘户型 |
|
|
成本价(万元/套) | 60 | 80 |
预售价(万元/套) | 80 | 120 |
若公司最多投入开发资金为14000万元,所获利润为![]() 万元,
万元,
(1)求![]() 与
与![]() 的函效关系式和自变量
的函效关系式和自变量![]() 的取值范围
的取值范围
(2)售完这批楼盘,公司所获得的最大利润是多少?
(3)公司在实际销售过程中,其他条件不变,![]() 户型每套销售价格提高
户型每套销售价格提高![]() (
(![]() )万元,且限定
)万元,且限定![]() 户型最多开发120套,则公司如何建房,利润最大?(注:利润=售价-成本.)
户型最多开发120套,则公司如何建房,利润最大?(注:利润=售价-成本.)